High-Level Interface¶
Compiler.types module¶
This module defines all types available in high-level programs. These include basic types such as secret integers or floating-point numbers and container types. A single instance of the former uses one or more so-called registers in the virtual machine while the latter use the so-called memory. For every register type, there is a corresponding dedicated memory.
Registers are used for computation, allocated on an ongoing basis,
and thread-specific. The memory is allocated statically and shared
between threads. This means that memory-based types such as
Array can be used to transfer information between threads.
Note that creating memory-based types outside the main thread is not
supported.
If viewing this documentation in processed form, many function signatures appear generic because of the use of decorators. See the source code for the correct signature.
Basic types¶
All basic types can be used as vectors, that is one instance representing several values, with all operations being executed element-wise. For example, the following computes ten multiplications of integers input by party 0 and 1:
sint.get_input_from(0, size=10) * sint.get_input_from(1, size=10)
Secret integer in the protocol-specific domain. |
|
Clear integer in same domain as secure computation (depends on protocol). |
|
Clear 64-bit integer. |
|
Secret fixed-point number represented as secret integer, by multiplying with |
|
Clear fixed-point number represented as clear integer. |
|
Secret floating-point number. |
|
Secret \(\mathrm{GF}(2^n)\) value. |
|
Clear \(\mathrm{GF}(2^n)\) value. |
|
Value known to one player. |
Container types¶
Single value in memory. |
|
Array accessible by public index. |
|
Matrix. |
|
Multidimensional array. |
- class Compiler.types.Array(length, value_type, address=None, debug=None, alloc=True)[source]¶
Array accessible by public index. That is,
a[i]works for an arrayaandibeing aregint,cint, or a Python integer.- Parameters
length – compile-time integer (int) or
Nonefor unknown length (need to specifyaddress)value_type – basic type
address – if given (regint/int), the array will not be allocated
You can convert between arrays and register vectors by using slice indexing. This allows for element-wise operations as long as supported by the basic type. The following adds 10 secret integers from the first two parties:
a = sint.Array(10) a.input_from(0) b = sint.Array(10) b.input_from(1) a[:] += b[:]
Arrays aren’t initialized on creation, you need to call
assign_all()to initialize them to a constant value.- assign(other, base=0)[source]¶
Assignment.
- Parameters
other – vector/Array/Matrix/MultiArray/iterable of compatible type and smaller size
base – index to start assignment at
- assign_all(value, n_threads=None, conv=True)[source]¶
Assign the same value to all entries.
- Parameters
value – convertible to basic type
- assign_part_vector(other, base=0)¶
Assignment.
- Parameters
other – vector/Array/Matrix/MultiArray/iterable of compatible type and smaller size
base – index to start assignment at
- assign_vector(other, base=0)¶
Assignment.
- Parameters
other – vector/Array/Matrix/MultiArray/iterable of compatible type and smaller size
base – index to start assignment at
- classmethod create_from(l)[source]¶
Convert Python iterator or vector to array. Basic type will be taken from first element, further elements must to be convertible to that.
- Parameters
l – Python iterable or register vector
- Returns
Arrayof appropriate type containing the contents ofl
- expand_to_vector(index, size)[source]¶
Create vector from single entry.
- Parameters
index – regint/cint/int
size – int
- get_part(base, size)[source]¶
Part array.
- Parameters
base – start index (regint/cint/int)
size – integer
- Returns
Array of same type
- get_part_vector(base=0, size=None)¶
Return vector with content.
- Parameters
base – starting point (regint/cint/int)
size – length (compile-time int)
- get_vector(base=0, size=None)[source]¶
Return vector with content.
- Parameters
base – starting point (regint/cint/int)
size – length (compile-time int)
- input_from(player, budget=None, raw=False, **kwargs)[source]¶
Fill with inputs from player if supported by type.
- Parameters
player – public (regint/cint/int)
- maybe_get(condition, index)[source]¶
Return entry if condition is true.
- Parameters
condition – 0/1 (regint/cint/int)
index – regint/cint/int
- maybe_set(condition, index, value)[source]¶
Change entry if condition is true.
- Parameters
condition – 0/1 (regint/cint/int)
index – regint/cint/int
value – updated value
- permute(permutation, reverse=False, n_threads=None)[source]¶
Public permutation.
- Parameters
permutation – cleartext :py:class`Array` containing number in \([0,n-1]\) where \(n\) is the length of this array
reverse – whether to apply the inverse of the permutation
- print_reveal_nested(end='\n')[source]¶
Reveal and print as list.
- Parameters
end – string to print after (default: line break)
- randomize(*args)[source]¶
Randomize array according to data type. If it is
sfix, the following will sample an individual uniformly random entry of the arrayMroughly in the range \([a,b]\):M.randomize(a, b)
- read_from_file(start)[source]¶
Read content from
Persistence/Transactions-P<playerno>.data. Precision must be the same as when storing if applicable. See this section for details on the data format.- Parameters
start – starting position in number of shares from beginning (int/regint/cint)
- Returns
destination for final position, -1 for eof reached, or -2 for file not found (regint)
- reveal_nested()¶
Reveal as list.
- reveal_to(player)[source]¶
Reveal secret array to
player.- Parameters
player – public integer (int/regint/cint)
- Returns
personalcontaining an array
- reveal_to_binary_output(player=None)[source]¶
Reveal to binary output if supported by type.
- Param
player to reveal to (default all)
- reveal_to_clients(clients)¶
Reveal contents to list of clients.
- Parameters
clients – list or array of client identifiers
- secure_permute(*args, **kwargs)[source]¶
Secure permute in place according to the security model. See
MultiArray.secure_shuffle()for references.- Parameters
permutation – output of
sint.get_secure_shuffle()reverse – whether to apply inverse (default: False)
- secure_shuffle()[source]¶
Secure shuffle in place according to the security model. See
MultiArray.secure_shuffle()for references.
- sort(n_threads=None, batcher=False, n_bits=None)[source]¶
Sort in place using radix sort with complexity \(O(n \log n)\) for
sintandsfix, and Batcher’s odd-even mergesort with \(O(n (\log n)^2)\) forsfloat.- Parameters
n_threads – number of threads to use (single thread by default), need to use Batcher’s algorithm for several threads
batcher – use Batcher’s odd-even mergesort in any case
n_bits – number of bits in keys (default: global bit length)
- write_to_file(position=None)[source]¶
Write shares of integer representation to
Persistence/Transactions-P<playerno>.data. See this section for details on the data format.- Parameters
position – start position (int/regint/cint), defaults to end of file
- class Compiler.types.Matrix(rows, columns, value_type, debug=None, address=None)[source]¶
Matrix.
- Parameters
rows – compile-time (int)
columns – compile-time (int)
value_type – basic type of entries
Matrices aren’t initialized on creation, you need to call
assign_all()to initialize them to a constant value.- assign(other, base=0)¶
Assign container to content. Not implemented for floating-point.
- Parameters
other – container of matching size and type
- assign_all(value)¶
Assign the same value to all entries.
- Parameters
value – convertible to relevant basic type
- assign_part_vector(vector, base=0)¶
Assign vector from range of the first dimension, including all entries in further dimensions.
- Parameters
vector – updated entries
base – index in first dimension (regint/cint/int)
- assign_vector(vector, base=0)¶
Assign vector to content. Not implemented for floating-point.
- Parameters
vector – vector of matching size convertible to relevant basic type
base – compile-time (int)
- assign_vector_by_indices(vector, *indices)¶
Assign vector to entries with potential asterisks. See
get_vector_by_indices()for an example.
- concat(other)¶
Concatenate two multi-arrays of matching dimension.
- diag()¶
Matrix diagonal.
- direct_mul(other, reduce=True, indices=None, res_type=None)¶
Matrix multiplication in the virtual machine. Unlike
dot(), this only works for sint and sfix, and it returns a vector instead of a data structure.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
The following executes a matrix multiplication selecting every third row of
A:A = sfix.Matrix(7, 4) B = sfix.Matrix(4, 5) C = sfix.Matrix(3, 5) C.assign_vector(A.direct_mul(B, indices=(regint.inc(3, 0, 3), regint.inc(4), regint.inc(4), regint.inc(5)))
- direct_mul_trans(other, reduce=True, indices=None)¶
Matrix multiplication with the transpose of
otherin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
- direct_trans_mul(other, reduce=True, indices=None)¶
Matrix multiplication with the transpose of
selfin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
- dot(other, res_params=None, n_threads=None)¶
Matrix-matrix and matrix-vector multiplication.
- Parameters
self – two-dimensional
other – Matrix or Array of matching size and type
n_threads – number of threads (default: all in same thread)
- Return type
Matrix or Array of appropriate size and type
- get_column(index)¶
Get matrix column as vector.
- Parameters
index – regint/cint/int
- get_part(start, size)¶
Part multi-array.
- Parameters
start – first-dimension index (regint/cint/int)
size – int
- get_part_vector(base=0, size=None)¶
Vector from range of the first dimension, including all entries in further dimensions.
- Parameters
base – index in first dimension (regint/cint/int)
size – size in first dimension (int)
- get_slice_vector(slice)¶
Vector from range of indicies of the first dimension, including all entries in further dimensions.
- Parameters
slice – regint array
- get_vector(base=0, size=None)¶
Return vector with content. Not implemented for floating-point.
- Parameters
base – public (regint/cint/int)
size – compile-time (int)
- get_vector_by_indices(*indices)¶
Vector with potential asterisks. The potential retrieves all entries where the first dimension index is 0, and the third dimension index is 1:
a.get_vector_by_indices(0, None, 1)
- iadd(other)¶
Element-wise addition in place.
- Parameters
other – container of matching size and type
- input_from(player, budget=None, raw=False, **kwargs)¶
Fill with inputs from player if supported by type.
- Parameters
player – public (regint/cint/int)
- mul_trans(other)¶
Matrix multiplication with transpose of
other.- Parameters
self – two-dimensional
other – two-dimensional container of matching type and size
- Returns
Matrix of matching type and size
- mul_trans_to(other, res, n_threads=None)¶
Matrix multiplication with the transpose of
otherin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayres – matrix of matching dimension to store result
n_threads – number of threads (default: single thread)
- permute(permutation, reverse=False, n_threads=None)¶
Public permutation along first dimension.
- Parameters
permutation – cleartext :py:class`Array` containing number in \([0,n-1]\) where \(n\) is the length of this array
reverse – whether to apply the inverse of the permutation
- print_reveal_nested(end='\n')¶
Reveal and print as nested list.
- Parameters
end – string to print after (default: line break)
- randomize(*args, n_threads=None)¶
Randomize according to data type. If it is
sfix, the following will sample an individual uniformly random entry of the multi-arrayMroughly in the range \([a,b]\):M.randomize(a, b)
- read_from_file(start)¶
Read content from
Persistence/Transactions-P<playerno>.data. Precision must be the same as when storing if applicable. See this section for details on the data format.- Parameters
start – starting position in number of shares from beginning (int/regint/cint)
- Returns
destination for final position, -1 for eof reached, or -2 for file not found (regint)
- read_from_socket(socket, debug=False)¶
Read content from socket.
- reveal()¶
Reveal to
MultiArrayof same shape.
- reveal_list()¶
Reveal as list.
- reveal_nested()¶
Reveal as nested list.
- reveal_to_binary_output(player=None)¶
Reveal to binary output if supported by type.
- Param
player to reveal to (default all)
- reveal_to_clients(clients)¶
Reveal contents to list of clients.
- Parameters
clients – list or array of client identifiers
- same_shape()¶
- Returns
new multidimensional array with same shape and basic type
- schur(other)¶
Element-wise product.
- Parameters
other – container of matching size and type
- Returns
container of same shape and type as
self
- secure_permute(permutation, reverse=False, n_threads=None)¶
Securely permute rows (first index). See
secure_shuffle()for references.- Parameters
permutation – output of
sint.get_secure_shuffle()reverse – whether to apply inverse (default: False)
- secure_shuffle()¶
Securely shuffle rows (first index). This uses the algorithm in Section 4.3 of Keller and Scholl or Section 3.2 of Asharov et al. if applicable.
- set_column(index, vector)¶
Change column.
- Parameters
index – regint/cint/int
vector – short enought vector of compatible type
- sort(key_indices=None, n_bits=None)¶
Sort sub-arrays (different first index) in place. This uses radix sort.
- Parameters
key_indices – indices to sorting keys, for example
(1, 2)to sort three-dimensional arrayaby keysa[*][1][2]. Default is(0, ..., 0)of correct length.n_bits – number of bits in keys (default: global bit length)
- trace()¶
Matrix trace.
- trans_mul(other)¶
Matrix multiplication with transpose of
self- Parameters
self – two-dimensional
other – two-dimensional container of matching type and size
- Returns
Matrix of matching type and size
- trans_mul_to(other, res, n_threads=None)¶
Matrix multiplication with the transpose of
selfin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayres – matrix of matching dimension to store result
n_threads – number of threads (default: single thread)
- transpose(n_threads=None)¶
Matrix transpose.
- Parameters
self – two-dimensional
- write_to_file(position=None)¶
Write shares of integer representation to
Persistence/Transactions-P<playerno>.data. See this section for details on the data format.- Parameters
position – start position (int/regint/cint), defaults to end of file
- write_to_socket(socket, debug=False)¶
Write content to socket.
- class Compiler.types.MemValue(value, address=None)[source]¶
Single value in memory. This is useful to transfer information between threads. Operations are automatically read from memory if required, this means you can use any operation with
MemValueobjects as if they were a basic type.- Parameters
value – basic type or int (will be converted to regint)
- iadd(other)¶
Addition assignment.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- square()¶
Square.
- class Compiler.types.MultiArray(sizes, value_type, debug=None, address=None, alloc=True)[source]¶
Multidimensional array. The access operator (
a[i]) allows to a multi-dimensional array of dimension one less or a simple array for a two-dimensional array.- Parameters
sizes – shape (compile-time list of integers)
value_type – basic type of entries
You can convert between arrays and register vectors by using slice indexing. This allows for element-wise operations as long as supported by the basic type. The following has the first two parties input a 10x10 secret integer matrix followed by storing the element-wise multiplications in the same data structure:
a = sint.Tensor([3, 10, 10]) a[0].input_from(0) a[1].input_from(1) a[2][:] = a[0][:] * a[1][:]
Arrays aren’t initialized on creation, you need to call
assign_all()to initialize them to a constant value.- assign(other, base=0)¶
Assign container to content. Not implemented for floating-point.
- Parameters
other – container of matching size and type
- assign_all(value)¶
Assign the same value to all entries.
- Parameters
value – convertible to relevant basic type
- assign_part_vector(vector, base=0)¶
Assign vector from range of the first dimension, including all entries in further dimensions.
- Parameters
vector – updated entries
base – index in first dimension (regint/cint/int)
- assign_vector(vector, base=0)¶
Assign vector to content. Not implemented for floating-point.
- Parameters
vector – vector of matching size convertible to relevant basic type
base – compile-time (int)
- assign_vector_by_indices(vector, *indices)¶
Assign vector to entries with potential asterisks. See
get_vector_by_indices()for an example.
- concat(other)¶
Concatenate two multi-arrays of matching dimension.
- diag()¶
Matrix diagonal.
- direct_mul(other, reduce=True, indices=None, res_type=None)¶
Matrix multiplication in the virtual machine. Unlike
dot(), this only works for sint and sfix, and it returns a vector instead of a data structure.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
The following executes a matrix multiplication selecting every third row of
A:A = sfix.Matrix(7, 4) B = sfix.Matrix(4, 5) C = sfix.Matrix(3, 5) C.assign_vector(A.direct_mul(B, indices=(regint.inc(3, 0, 3), regint.inc(4), regint.inc(4), regint.inc(5)))
- direct_mul_trans(other, reduce=True, indices=None)¶
Matrix multiplication with the transpose of
otherin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
- direct_trans_mul(other, reduce=True, indices=None)¶
Matrix multiplication with the transpose of
selfin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayindices – 4-tuple of
regintvectors for index selection (default is complete multiplication)
- Returns
Matrix as vector of relevant type (row-major)
- dot(other, res_params=None, n_threads=None)¶
Matrix-matrix and matrix-vector multiplication.
- Parameters
self – two-dimensional
other – Matrix or Array of matching size and type
n_threads – number of threads (default: all in same thread)
- Return type
Matrix or Array of appropriate size and type
- get_column(index)¶
Get matrix column as vector.
- Parameters
index – regint/cint/int
- get_part(start, size)¶
Part multi-array.
- Parameters
start – first-dimension index (regint/cint/int)
size – int
- get_part_vector(base=0, size=None)¶
Vector from range of the first dimension, including all entries in further dimensions.
- Parameters
base – index in first dimension (regint/cint/int)
size – size in first dimension (int)
- get_slice_vector(slice)¶
Vector from range of indicies of the first dimension, including all entries in further dimensions.
- Parameters
slice – regint array
- get_vector(base=0, size=None)¶
Return vector with content. Not implemented for floating-point.
- Parameters
base – public (regint/cint/int)
size – compile-time (int)
- get_vector_by_indices(*indices)¶
Vector with potential asterisks. The potential retrieves all entries where the first dimension index is 0, and the third dimension index is 1:
a.get_vector_by_indices(0, None, 1)
- iadd(other)¶
Element-wise addition in place.
- Parameters
other – container of matching size and type
- input_from(player, budget=None, raw=False, **kwargs)¶
Fill with inputs from player if supported by type.
- Parameters
player – public (regint/cint/int)
- mul_trans(other)¶
Matrix multiplication with transpose of
other.- Parameters
self – two-dimensional
other – two-dimensional container of matching type and size
- Returns
Matrix of matching type and size
- mul_trans_to(other, res, n_threads=None)¶
Matrix multiplication with the transpose of
otherin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayres – matrix of matching dimension to store result
n_threads – number of threads (default: single thread)
- permute(permutation, reverse=False, n_threads=None)¶
Public permutation along first dimension.
- Parameters
permutation – cleartext :py:class`Array` containing number in \([0,n-1]\) where \(n\) is the length of this array
reverse – whether to apply the inverse of the permutation
- print_reveal_nested(end='\n')¶
Reveal and print as nested list.
- Parameters
end – string to print after (default: line break)
- randomize(*args, n_threads=None)¶
Randomize according to data type. If it is
sfix, the following will sample an individual uniformly random entry of the multi-arrayMroughly in the range \([a,b]\):M.randomize(a, b)
- read_from_file(start)¶
Read content from
Persistence/Transactions-P<playerno>.data. Precision must be the same as when storing if applicable. See this section for details on the data format.- Parameters
start – starting position in number of shares from beginning (int/regint/cint)
- Returns
destination for final position, -1 for eof reached, or -2 for file not found (regint)
- read_from_socket(socket, debug=False)¶
Read content from socket.
- reveal()¶
Reveal to
MultiArrayof same shape.
- reveal_list()¶
Reveal as list.
- reveal_nested()¶
Reveal as nested list.
- reveal_to_binary_output(player=None)¶
Reveal to binary output if supported by type.
- Param
player to reveal to (default all)
- reveal_to_clients(clients)¶
Reveal contents to list of clients.
- Parameters
clients – list or array of client identifiers
- same_shape()¶
- Returns
new multidimensional array with same shape and basic type
- schur(other)¶
Element-wise product.
- Parameters
other – container of matching size and type
- Returns
container of same shape and type as
self
- secure_permute(permutation, reverse=False, n_threads=None)¶
Securely permute rows (first index). See
secure_shuffle()for references.- Parameters
permutation – output of
sint.get_secure_shuffle()reverse – whether to apply inverse (default: False)
- secure_shuffle()¶
Securely shuffle rows (first index). This uses the algorithm in Section 4.3 of Keller and Scholl or Section 3.2 of Asharov et al. if applicable.
- set_column(index, vector)¶
Change column.
- Parameters
index – regint/cint/int
vector – short enought vector of compatible type
- sort(key_indices=None, n_bits=None)¶
Sort sub-arrays (different first index) in place. This uses radix sort.
- Parameters
key_indices – indices to sorting keys, for example
(1, 2)to sort three-dimensional arrayaby keysa[*][1][2]. Default is(0, ..., 0)of correct length.n_bits – number of bits in keys (default: global bit length)
- trace()¶
Matrix trace.
- trans_mul(other)¶
Matrix multiplication with transpose of
self- Parameters
self – two-dimensional
other – two-dimensional container of matching type and size
- Returns
Matrix of matching type and size
- trans_mul_to(other, res, n_threads=None)¶
Matrix multiplication with the transpose of
selfin the virtual machine.- Parameters
self –
Matrix/ 2-dimensionalMultiArrayother –
Matrix/ 2-dimensionalMultiArrayres – matrix of matching dimension to store result
n_threads – number of threads (default: single thread)
- transpose(n_threads=None)¶
Matrix transpose.
- Parameters
self – two-dimensional
- write_to_file(position=None)¶
Write shares of integer representation to
Persistence/Transactions-P<playerno>.data. See this section for details on the data format.- Parameters
position – start position (int/regint/cint), defaults to end of file
- write_to_socket(socket, debug=False)¶
Write content to socket.
- class Compiler.types.cfix(**kwargs)[source]¶
Clear fixed-point number represented as clear integer. It supports basic arithmetic (
+, -, *, /), returning eithercfixif the other operand is public (cfix/regint/cint/int) orsfixif the other operand is an sfix. It also support comparisons (==, !=, <, <=, >, >=), returning eitherregintorsbitint.- Parameters
v – cfix/float/int
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- binary_output(player=None)[source]¶
Write double-precision floating-point number to
Player-Data/Binary-Output-P<playerno>-<threadno>.- Parameters
player – only output on given player (default all)
- iadd(other)¶
Addition assignment. This uses
update()internally.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- classmethod read_from_socket(*args, **kwargs)[source]¶
Receive clear fixed-point value(s) from client. The client needs to convert the values to the right integer representation.
- Parameters
client_id – Client id (regint)
n – number of values (default 1)
- Param
vector size (int)
- Returns
cfix (if n=1) or list of cfix
- classmethod set_precision(f, k=None)[source]¶
Set the precision of the integer representation. The initial defaults are chosen to allow the best optimization of probabilistic truncation in computation modulo 2^64 (2*k < 64). Generally, 2*k must be at most the integer length for rings and at most m-s-1 for computation modulo an m-bit prime and statistical security s (default 40).
- Parameters
f – bit length of decimal part (initial default 16)
k – whole bit length of fixed point, defaults to twice
fif not given (initial default 31)
- square()¶
Square.
- class Compiler.types.cfloat(**kwargs)[source]¶
Helper class for printing revealed sfloats.
- class Compiler.types.cgf2n(val=None, size=None)[source]¶
Clear \(\mathrm{GF}(2^n)\) value. n is chosen at runtime. A number operators are supported (
+, -, *, /, **, ^, &, |, ~, ==, !=, <<, >>), returning eithercgf2nif the other operand is public (cgf2n/regint/int) orsgf2nif the other operand is secret. The following operators require the other operand to be a compile-time integer:**, <<, >>.*, /, **refer to field multiplication and division.- Parameters
val – initialization (cgf2n/cint/regint/int or list thereof)
size – vector size (int), defaults to 1 or size of list
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- binary_output(*args, **kwargs)¶
Write 64-bit signed integer to
Player-Data/Binary-Output-P<playerno>-<threadno>.- Parameters
player – only output on given player (default all)
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod bit_compose(bits, step=None)[source]¶
Clear \(\mathrm{GF}(2^n)\) bit composition.
- Parameters
bits – list of cgf2n
step – set every
step-th bit in output (defaults to 1)
- bit_decompose(*args, **kwargs)[source]¶
Clear bit decomposition.
- Parameters
bit_length – number of bits (defaults to global \(\mathrm{GF}(2^n)\) bit length)
step – extract every
step-th bit (defaults to 1)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in \(\mathrm{GF}(2^n)\) circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- cond_swap(a, b, t=None)¶
Swapping in \(\mathrm{GF}(2^n)\). Similar to
_int.if_else().
- field_div(other)¶
Field division of public values. Not available for computation modulo a power of two.
- Parameters
other – convertible type (at least same as
selfand regint/int)
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(a, b)¶
MUX in \(\mathrm{GF}(2^n)\) circuits. Similar to
_int.if_else().
- classmethod malloc(size, creator_tape=None, **kwargs)¶
Allocate memory (statically).
- Parameters
size – compile-time (int)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- print_reg_plain(*args, **kwargs)¶
Output.
- reveal()¶
Identity.
- square()¶
Square.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.types.cint(**kwargs)[source]¶
Clear integer in same domain as secure computation (depends on protocol). A number operators are supported (
+, -, *, /, //, **, %, ^, &, |, ~, ==, !=, <<, >>), returning eithercintif the other operand is public (cint/regint/int) orsintif the other operand issint. Comparison operators (==, !=, <, <=, >, >=) are also supported, returningregint(). Comparisons and~require that the value is within the global bit length. The same holds forabs()./runs field division if the modulus is a prime while//runs integer floor division.**requires the exponent to be compile-time integer or the base to be two.- Parameters
val – initialization (cint/regint/int/cgf2n or list thereof)
size – vector size (int), defaults to 1 or size of list
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- binary_output(*args, **kwargs)¶
Write 64-bit signed integer to
Player-Data/Binary-Output-P<playerno>-<threadno>.- Parameters
player – only output on given player (default all)
- static bit_adder(*args, **kwargs)¶
Binary adder in arithmetic circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
Single-bit AND in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod bit_compose(bits)¶
Compose value from bits.
- Parameters
bits – iterable of any type implementing left shift
- bit_decompose(*args, **kwargs)[source]¶
Clear bit decomposition.
- Parameters
bit_length – number of bits (default is global bit length)
- Returns
list of cint
- bit_not()¶
Single-bit NOT in arithmetic circuits.
- bit_or(other)¶
Single-bit OR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
Single-bit XOR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- cond_swap(a, b)¶
Swapping in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
(a, b)ifselfis 0,(b, a)ifselfis 1, and undefined otherwise- Return type
depending on operands, secret if any of them is
- field_div(other)¶
Field division of public values. Not available for computation modulo a power of two.
- Parameters
other – convertible type (at least same as
selfand regint/int)
- half_adder(other)¶
Half adder in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs, secret if any is
- if_else(a, b)¶
MUX on bit in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
a if
selfis 1, b ifselfis 0, undefined otherwise- Return type
depending on operands, secret if any of them is
- less_than(*args, **kwargs)[source]¶
Clear comparison for particular bit length.
- Parameters
other – cint/regint/int
bit_length – signed bit length of inputs
- Returns
0/1 (regint), undefined if inputs outside range
- classmethod malloc(size, creator_tape=None, **kwargs)¶
Allocate memory (statically).
- Parameters
size – compile-time (int)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- print_reg_plain(*args, **kwargs)¶
Output.
- classmethod read_from_socket(*args, **kwargs)[source]¶
Receive clear value(s) from client.
- Parameters
client_id – Client id (regint)
n – number of values (default 1)
size – vector size (default 1)
- Returns
cint (if n=1) or list of cint
- reveal()¶
Identity.
- square()¶
Square.
- to_regint(*args, **kwargs)[source]¶
Convert to regint.
- Parameters
n_bits – bit length (int)
- Returns
regint
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.types.localint(value=None)[source]¶
Local integer that must prevented from leaking into the secure computation. Uses regint internally.
- Parameters
value – initialization, convertible to regint
- class Compiler.types.personal(player, value)[source]¶
Value known to one player. Supports operations with public values and personal values known to the same player. Can be used with
print_ln_to(). It is possible to convert to secret types likesint.- Parameters
player – player (int)
value – cleartext value (cint, cfix, cfloat) or array thereof
- binary_output()[source]¶
Write binary output to
Player-Data/Binary-Output-P<playerno>-<threadno>if supported by underlying type. Player must be known at compile time.
- classmethod read_fix(player, f, k, precision)[source]¶
Read fixed-point value from
Player-Data/Input-Binary-P<player>-<threadnum>only on partyplayer.- Parameters
player – player (int)
f – fixed-point precision (int)
k – fixed-point length (int)
precision – input precision (1: single, 2: double)
- Returns
personal cfix
- class Compiler.types.regint(**kwargs)[source]¶
Clear 64-bit integer. Unlike
cintthis is always a 64-bit integer. The type supports the following operations withregintor Python integers, always returningregint:+, -, *, %, /, //, **, ^, &, |, <<, >>, ==, !=, <, <=, >, >=. For operations with other types, see the respective descriptions. Both/and//stand for floor division.- Parameters
val – initialization (cint/cgf2n/regint/int or list thereof)
size – vector size (int), defaults to 1 or size of list
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- binary_output(player=None)[source]¶
Write 64-bit signed integer to
Player-Data/Binary-Output-P<playerno>-<threadno>.- Parameters
player – only output on given player (default all)
- static bit_adder(*args, **kwargs)¶
Binary adder in arithmetic circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
Single-bit AND in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_decompose(*args, **kwargs)[source]¶
Clear bit decomposition.
- Parameters
bit_length – number of bits (defaults to global bit length)
- Returns
list of regint
- bit_not()¶
Single-bit NOT in arithmetic circuits.
- bit_or(other)¶
Single-bit OR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
Single-bit XOR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- cond_swap(a, b)¶
Swapping in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
(a, b)ifselfis 0,(b, a)ifselfis 1, and undefined otherwise- Return type
depending on operands, secret if any of them is
- classmethod get_random(*args, **kwargs)[source]¶
Public insecure randomness.
- Parameters
bit_length – number of bits (int)
size – vector size (int, default 1)
- half_adder(other)¶
Half adder in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs, secret if any is
- if_else(a, b)¶
MUX on bit in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
a if
selfis 1, b ifselfis 0, undefined otherwise- Return type
depending on operands, secret if any of them is
- classmethod inc(size, base=0, step=1, repeat=1, wrap=None)[source]¶
Produce
regintvector with certain patterns. This is particularly useful forSubMultiArray.direct_mul().- Parameters
size – Result size
base – First value
step – Increase step
repeat – Repeate this many times
wrap – Start over after this many increases
The following produces (1, 1, 1, 3, 3, 3, 5, 5, 5, 7):
regint.inc(10, 1, 2, 3)
- classmethod malloc(size, creator_tape=None, **kwargs)¶
Allocate memory (statically).
- Parameters
size – compile-time (int)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- classmethod push(*args, **kwargs)[source]¶
Push to stack. Made obsolete by
update().- Parameters
value – any convertible type
- classmethod read_from_socket(*args, **kwargs)[source]¶
Receive clear integer value(s) from client.
- Parameters
client_id – Client id (regint)
n – number of values (default 1)
size – vector size (default 1)
- Returns
regint (if n=1) or list of regint
- square()¶
Square.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.types.sfix(**kwargs)[source]¶
Secret fixed-point number represented as secret integer, by multiplying with
2^fand then rounding. Seesintfor security considerations of the underlying integer operations. The secret integer is stored as thevmember.It supports basic arithmetic (
+, -, *, /), returningsfix, and comparisons (==, !=, <, <=, >, >=), returningsbitint. The other operand can be any of sfix/sint/cfix/regint/cint/int/float. It also supportsabs()and**.Note that the default precision (16 bits after the dot, 31 bits in total) only allows numbers up to \(2^{31-16-1} \approx 16000\). You can increase this using
set_precision().- Params _v
int/float/regint/cint/sint/sfloat
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- bit_decompose(n_bits=None)¶
Bit decomposition.
- compute_reciprocal(*args, **kwargs)¶
Secret fixed-point reciprocal.
- classmethod dot_product(x, y, res_params=None)[source]¶
Secret dot product.
- Parameters
x – iterable of appropriate secret type
y – iterable of appropriate secret type and same length
- classmethod get_input_from(*args, **kwargs)[source]¶
Secret fixed-point input.
- Parameters
player – public (regint/cint/int)
size – vector size (int, default 1)
- classmethod get_random(*args, **kwargs)[source]¶
Uniform secret random number around centre of bounds. Actual range can be smaller but never larger.
- Parameters
lower – float
upper – float
symmetric – symmetric distribution at higher cost
public_randomness – use public randomness (avoids preprocessing)
size – vector size (int, default 1)
- classmethod input_tensor_from(player, shape)¶
Input tensor secretly from player.
- Parameters
player – int/regint/cint
shape – tensor shape
- classmethod input_tensor_from_client(client_id, shape)¶
Input tensor secretly from client.
- Parameters
client_id – client identifier (public)
shape – tensor shape
- classmethod input_tensor_via(player, content=None, shape=None, binary=True, one_hot=False, skip_input=False, n_bytes=None)¶
Input tensor-like data via a player. This overwrites the input file for the relevant player. The following returns an
sintmatrix of dimension 2 by 2:M = [[1, 2], [3, 4]] sint.input_tensor_via(0, M)
Make sure to copy
Player-Data/Input-P<player>-0orPlayer-Data/Input-Binary-P<player>-0if running on another host.- Parameters
player – player to input via (int)
content – nested Python list or numpy array (binary mode only) or left out if not available
shape – shape if content not given
binary – binary mode (bool)
one_hot – one-hot encoding (bool)
- classmethod load_mem(*args, **kwargs)¶
Load from memory by public address.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- classmethod read_from_file(*args, **kwargs)¶
Read shares from
Persistence/Transactions-P<playerno>.data. Precision must be the same as when storing. See this section for details on the data format.- Parameters
start – starting position in number of shares from beginning (int/regint/cint)
n_items – number of items (int)
- Returns
destination for final position, -1 for eof reached, or -2 for file not found (regint)
- Returns
list of shares
- classmethod receive_from_client(*args, **kwargs)¶
Securely obtain shares of values input by a client via
sint.receive_from_client(). Assumes client has already converted values to integer representation.- Parameters
n – number of inputs (int)
client_id – regint
size – vector size (default 1)
- Returns
list of length
n
- reveal()¶
Reveal secret fixed-point number.
- Returns
relevant clear type
- reveal_to(player)[source]¶
Reveal secret value to
player.- Parameters
player – public integer (int/regint/cint)
- Returns
- classmethod reveal_to_clients(clients, values)¶
Reveal securely to clients via
sint.reveal_to_clients().- Parameters
clients – client ids (list or array)
values – list of values of this class
- classmethod set_precision(f, k=None)¶
Set the precision of the integer representation. The initial defaults are chosen to allow the best optimization of probabilistic truncation in computation modulo 2^64 (2*k < 64). Generally, 2*k must be at most the integer length for rings and at most m-s-1 for computation modulo an m-bit prime and statistical security s (default 40).
- Parameters
f – bit length of decimal part (initial default 16)
k – whole bit length of fixed point, defaults to twice
fif not given (initial default 31)
- square()¶
Square.
- store_in_mem(address)¶
Store in memory by public address.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
Send shares of integer representations of a list of values to a specified client socket.
- Parameters
client_id – regint
values – list of values of this type
- classmethod write_to_file(shares, position=None)¶
Write shares of integer representation to
Persistence/Transactions-P<playerno>.data. See this section for details on the data format.- Parameters
shares – (list or iterable of sfix)
position – start position (int/regint/cint), defaults to end of file
- class Compiler.types.sfloat(**kwargs)[source]¶
Secret floating-point number. Represents \((1 - 2s) \cdot (1 - z)\cdot v \cdot 2^p\).
v: significand
p: exponent
z: zero flag
s: sign bit
This uses integer operations internally, see
sintfor security considerations. See Aliasgari et al. for details.The type supports basic arithmetic (
+, -, *, /), returningsfloat, and comparisons (==, !=, <, <=, >, >=), returningsint. The other operand can be any of sint/cfix/regint/cint/int/float.This data type only works with arithmetic computation.
- Parameters
v – initialization (sfloat/sfix/float/int/sint/cint/regint)
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- classmethod get_input_from(*args, **kwargs)[source]¶
Secret floating-point input.
- Parameters
player – public (regint/cint/int)
size – vector size (int, default 1)
- classmethod input_tensor_from(player, shape)¶
Input tensor secretly from player.
- Parameters
player – int/regint/cint
shape – tensor shape
- classmethod input_tensor_from_client(client_id, shape)¶
Input tensor secretly from client.
- Parameters
client_id – client identifier (public)
shape – tensor shape
- classmethod input_tensor_via(player, content=None, shape=None, binary=True, one_hot=False, skip_input=False, n_bytes=None)¶
Input tensor-like data via a player. This overwrites the input file for the relevant player. The following returns an
sintmatrix of dimension 2 by 2:M = [[1, 2], [3, 4]] sint.input_tensor_via(0, M)
Make sure to copy
Player-Data/Input-P<player>-0orPlayer-Data/Input-Binary-P<player>-0if running on another host.- Parameters
player – player to input via (int)
content – nested Python list or numpy array (binary mode only) or left out if not available
shape – shape if content not given
binary – binary mode (bool)
one_hot – one-hot encoding (bool)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- square()¶
Square.
- update(other)[source]¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.types.sgf2n(**kwargs)[source]¶
Secret \(\mathrm{GF}(2^n)\) value. n is chosen at runtime. A number operators are supported (
+, -, *, /, **, ^, ~, ==, !=, <<),sgf2n. Operators generally work with cgf2n/regint/cint/int, except**, <<, which require a compile-time integer./refers to field division.*, /, **refer to field multiplication and division.- Parameters
val – initialization (sgf2n/cgf2n/regint/int/cint or list thereof)
size – vector size (int), defaults to 1 or size of list
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod bit_compose(bits)¶
Compose value from bits.
- Parameters
bits – iterable of any type convertible to sint
- bit_decompose(*args, **kwargs)[source]¶
Secret bit decomposition.
- Parameters
bit_length – number of bits
step – use every
step-th bit
- Returns
list of sgf2n
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in \(\mathrm{GF}(2^n)\) circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- cond_swap(a, b, t=None)¶
Swapping in \(\mathrm{GF}(2^n)\). Similar to
_int.if_else().
- classmethod dot_product(*args, **kwargs)¶
Secret dot product.
- Parameters
x – Iterable of secret values
y – Iterable of secret values of same length and type
- Return type
same as inputs
- equal(other, bit_length=None, expand=1)[source]¶
Secret comparison.
- Parameters
other – sgf2n/cgf2n/regint/int
- Returns
0/1 (sgf2n)
- field_div(other)¶
Secret field division.
- Parameters
other – any compatible type
- classmethod get_input_from(*args, **kwargs)¶
Secret input from player.
- Parameters
player – public (regint/cint/int)
size – vector size (int, default 1)
- classmethod get_random_bit(*args, **kwargs)¶
Secret random bit according to security model.
- Returns
0/1 50-50
- Parameters
size – vector size (int, default 1)
- classmethod get_random_input_mask_for(*args, **kwargs)¶
Secret random input mask according to security model.
- Returns
mask (sint), mask (personal cint)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_inverse(*args, **kwargs)¶
Secret random inverse tuple according to security model.
- Returns
\((a, a^{-1})\)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_square(*args, **kwargs)¶
Secret random square according to security model.
- Returns
\((a, a^2)\)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_triple(*args, **kwargs)¶
Secret random triple according to security model.
- Returns
\((a, b, ab)\)
- Parameters
size – vector size (int, default 1)
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(a, b)¶
MUX in \(\mathrm{GF}(2^n)\) circuits. Similar to
_int.if_else().
- classmethod input_tensor_from(player, shape)¶
Input tensor secretly from player.
- Parameters
player – int/regint/cint
shape – tensor shape
- classmethod input_tensor_from_client(client_id, shape)¶
Input tensor secretly from client.
- Parameters
client_id – client identifier (public)
shape – tensor shape
- classmethod input_tensor_via(player, content=None, shape=None, binary=True, one_hot=False, skip_input=False, n_bytes=None)¶
Input tensor-like data via a player. This overwrites the input file for the relevant player. The following returns an
sintmatrix of dimension 2 by 2:M = [[1, 2], [3, 4]] sint.input_tensor_via(0, M)
Make sure to copy
Player-Data/Input-P<player>-0orPlayer-Data/Input-Binary-P<player>-0if running on another host.- Parameters
player – player to input via (int)
content – nested Python list or numpy array (binary mode only) or left out if not available
shape – shape if content not given
binary – binary mode (bool)
one_hot – one-hot encoding (bool)
- classmethod malloc(size, creator_tape=None, **kwargs)¶
Allocate memory (statically).
- Parameters
size – compile-time (int)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- not_equal(other, bit_length=None)[source]¶
Secret comparison.
- Parameters
other – sgf2n/cgf2n/regint/int
- Returns
0/1 (sgf2n)
- raw_right_shift(*args, **kwargs)¶
Local right shift in supported protocols. In integer-like protocols, the output is potentially off by one.
- Parameters
length – number of bits
- reveal(*args, **kwargs)¶
Reveal secret value publicly.
- Return type
relevant clear type
- right_shift(*args, **kwargs)[source]¶
Secret right shift by public value:
- Parameters
other – compile-time (int)
bit_length – number of bits of
self(defaults to \(\mathrm{GF}(2^n)\) bit length)
- square(*args, **kwargs)¶
Secret square.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.types.sint(**kwargs)[source]¶
Secret integer in the protocol-specific domain. It supports operations with
sint,cint,regint, and Python integers. Operations where one of the operands is ansinteither result in ansintor ansintbit, the latter for comparisons.The following operations work as expected in the computation domain (modulo a prime or a power of two):
+, -, *./denotes a fixed-point division. Comparisons operators (==, !=, <, <=, >, >=) assume that the element in the computation domain represents a signed integer in a restricted range, see below. The same holds forabs(), shift operators (<<, >>), modulo (%), and exponentation (**). Modulo only works if the right-hand operator is a compile-time power of two.Most non-linear operations require compile-time parameters for bit length and statistical security. They default to the global parameters set by
program.set_bit_length()andprogram.set_security(). The acceptable minimum for statistical security is considered to be 40. The defaults for the parameters is output at the beginning of the compilation.If the computation domain is modulo a power of two, the operands will be truncated to the bit length, and the security parameter does not matter. Modulo prime, the behaviour is undefined and potentially insecure if the operands are longer than the bit length.
- Parameters
val – initialization (sint/cint/regint/int/cgf2n or list thereof, sbits/sbitvec/sfix, or
personal)size – vector size (int), defaults to 1 or size of list
When converting
sbits, the result is a vector of bits, and when convertingsbitvec, the result is a vector of values with bit length equal the length of the input.Initializing from a
personalvalue implies the relevant party inputting their value securely.- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod Matrix(rows, columns, *args, **kwargs)¶
Type-dependent matrix. Example:
a = sint.Matrix(10, 10)
- classmethod Tensor(shape)¶
Type-dependent tensor of any dimension:
a = sfix.Tensor([10, 10])
- static bit_adder(*args, **kwargs)¶
Binary adder in arithmetic circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
Single-bit AND in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod bit_compose(bits)¶
Compose value from bits.
- Parameters
bits – iterable of any type convertible to sint
- bit_not()¶
Single-bit NOT in arithmetic circuits.
- bit_or(other)¶
Single-bit OR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
Single-bit XOR in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- cond_swap(a, b)¶
Swapping in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
(a, b)ifselfis 0,(b, a)ifselfis 1, and undefined otherwise- Return type
depending on operands, secret if any of them is
- classmethod dot_product(*args, **kwargs)¶
Secret dot product.
- Parameters
x – Iterable of secret values
y – Iterable of secret values of same length and type
- Return type
same as inputs
- equal(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- field_div(other)¶
Secret field division.
- Parameters
other – any compatible type
- classmethod get_dabit(*args, **kwargs)[source]¶
Bit in arithmetic and binary circuit according to security model
- classmethod get_input_from(*args, **kwargs)[source]¶
Secret input.
- Parameters
player – public (regint/cint/int)
size – vector size (int, default 1)
- classmethod get_random(*args, **kwargs)[source]¶
Secret random ring element according to security model.
- Parameters
size – vector size (int, default 1)
- classmethod get_random_bit(*args, **kwargs)¶
Secret random bit according to security model.
- Returns
0/1 50-50
- Parameters
size – vector size (int, default 1)
- classmethod get_random_input_mask_for(*args, **kwargs)¶
Secret random input mask according to security model.
- Returns
mask (sint), mask (personal cint)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_int(*args, **kwargs)[source]¶
Secret random n-bit number according to security model.
- Parameters
bits – compile-time integer (int)
size – vector size (int, default 1)
- classmethod get_random_inverse(*args, **kwargs)¶
Secret random inverse tuple according to security model.
- Returns
\((a, a^{-1})\)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_square(*args, **kwargs)¶
Secret random square according to security model.
- Returns
\((a, a^2)\)
- Parameters
size – vector size (int, default 1)
- classmethod get_random_triple(*args, **kwargs)¶
Secret random triple according to security model.
- Returns
\((a, b, ab)\)
- Parameters
size – vector size (int, default 1)
- greater_equal(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- greater_than(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- half_adder(other)¶
Half adder in arithmetic circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs, secret if any is
- if_else(a, b)¶
MUX on bit in arithmetic circuits.
- Parameters
a/b – any type supporting the necessary operations
- Returns
a if
selfis 1, b ifselfis 0, undefined otherwise- Return type
depending on operands, secret if any of them is
- classmethod input_tensor_from(player, shape)¶
Input tensor secretly from player.
- Parameters
player – int/regint/cint
shape – tensor shape
- classmethod input_tensor_from_client(client_id, shape)¶
Input tensor secretly from client.
- Parameters
client_id – client identifier (public)
shape – tensor shape
- classmethod input_tensor_via(player, content=None, shape=None, binary=True, one_hot=False, skip_input=False, n_bytes=None)¶
Input tensor-like data via a player. This overwrites the input file for the relevant player. The following returns an
sintmatrix of dimension 2 by 2:M = [[1, 2], [3, 4]] sint.input_tensor_via(0, M)
Make sure to copy
Player-Data/Input-P<player>-0orPlayer-Data/Input-Binary-P<player>-0if running on another host.- Parameters
player – player to input via (int)
content – nested Python list or numpy array (binary mode only) or left out if not available
shape – shape if content not given
binary – binary mode (bool)
one_hot – one-hot encoding (bool)
- int_div(*args, **kwargs)[source]¶
Secret integer division. Note that the domain bit length needs to be about four times the bit length.
- Parameters
other – sint
bit_length – bit length of input (default: global bit length)
- int_mod(*args, **kwargs)[source]¶
Secret integer modulo. Note that the domain bit length needs to be about four times the bit length.
- Parameters
other – sint
bit_length – bit length of input (default: global bit length)
- left_shift(other, bit_length=None, security=None)¶
Secret left shift.
- Parameters
other – secret or public integer (sint/cint/regint/int)
bit_length – bit length of input (default: global bit length)
- less_equal(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- less_than(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- classmethod malloc(size, creator_tape=None, **kwargs)¶
Allocate memory (statically).
- Parameters
size – compile-time (int)
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- mod2m(*args, **kwargs)[source]¶
Secret modulo power of two.
- Parameters
m – secret or public integer (sint/cint/regint/int)
bit_length – bit length of input (default: global bit length)
- not_equal(*args, **kwargs)¶
Secret comparison (signed).
- Parameters
other – sint/cint/regint/int
bit_length – bit length of input (default: global bit length)
- Returns
0/1 (sintbit)
- pow2(*args, **kwargs)[source]¶
Secret power of two.
- Parameters
bit_length – bit length of input (default: global bit length)
- private_division(divisor, active=None, dividend_length=None, divisor_length=None)[source]¶
Private integer division as per Veugen and Abspoel
- Parameters
divisor – public (cint/regint) or personal value thereof
active – whether to check on the party knowing the divisor (active security)
dividend_length – bit length of the dividend (default: global bit length)
dividend_length – bit length of the divisor (default: global bit length)
- raw_right_shift(*args, **kwargs)¶
Local right shift in supported protocols. In integer-like protocols, the output is potentially off by one.
- Parameters
length – number of bits
- classmethod read_from_file(start, n_items)[source]¶
Read shares from
Persistence/Transactions-P<playerno>.data. See this section for details on the data format.- Parameters
start – starting position in number of shares from beginning (int/regint/cint)
n_items – number of items (int)
- Returns
destination for final position, -1 for eof reached, or -2 for file not found (regint)
- Returns
list of shares
- classmethod read_from_socket(*args, **kwargs)[source]¶
Receive secret-shared value(s) from client.
- Parameters
client_id – Client id (regint)
n – number of values (default 1)
size – vector size of values (default 1)
- Returns
sint (if n=1) or list of sint
- classmethod receive_from_client(*args, **kwargs)[source]¶
Securely obtain shares of values input by a client. This uses the triple-based input protocol introduced by Damgård et al. unless
program.activeis set to false, in which case it uses random values to mask the clients’ input.- Parameters
n – number of inputs (int)
client_id – regint
size – vector size (default 1)
- Returns
list of sint
- reveal(*args, **kwargs)¶
Reveal secret value publicly.
- Return type
relevant clear type
- reveal_to(player)[source]¶
Reveal secret value to
player.- Parameters
player – public integer (int/regint/cint)
- Returns
- classmethod reveal_to_clients(clients, values)[source]¶
Reveal securely to clients. Uses
program.activeto determine whether to use triples for active security.- Parameters
clients – client ids (list or array)
values – list of sint to reveal
- right_shift(*args, **kwargs)¶
Secret right shift.
- Parameters
other – secret or public integer (sint/cint/regint/int)
bit_length – bit length of input (default: global bit length)
- round(*args, **kwargs)[source]¶
Truncate and maybe round secret
k-bit integer bymbits.mcan be secret ifnearestis false, in which case the truncation will be exact. For publicm,nearestchooses between nearest rounding (rounding half up) and probablistic truncation.- Parameters
k – int
m – secret or compile-time integer (sint/int)
kappa – statistical security parameter (int)
nearest – bool
signed – bool
- square(*args, **kwargs)¶
Secret square.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
Send shares of a list of values to a specified client socket.
- Parameters
client_id – regint
values – list of sint
- static write_to_file(shares, position=None)[source]¶
Write shares to
Persistence/Transactions-P<playerno>.data(appending at the end). See this section for details on the data format.- Parameters
shares – (list or iterable of sint)
position – start position (int/regint/cint), defaults to end of file
Compiler.GC.types module¶
This modules contains basic types for binary circuits. The
fixed-length types obtained by get_type(n) are the preferred
way of using them, and in some cases required in connection with
container types.
Computation using these types will always be executed as a binary circuit. See Protocol Pairs for the exact protocols.
- class Compiler.GC.types.cbits(value=None, n=None, size=None)[source]¶
Clear bits register. Helper type with limited functionality.
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod get_type(length)¶
Returns a fixed-length type.
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(x, y)¶
Vectorized oblivious selection:
sb32 = sbits.get_type(32) print_ln('%s', sb32(3).if_else(sb32(5), sb32(2)).reveal())
This will output 1.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbit(*args, **kwargs)[source]¶
Single secret bit.
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- static bit_adder(*args, **kwargs)¶
Binary adder in binary circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod get_input_from(player, n_bits=None)¶
Secret input from
player.- Param
player (int)
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(x, y)[source]¶
Non-vectorized oblivious selection:
sb32 = sbits.get_type(32) print_ln('%s', sbit(1).if_else(sb32(5), sb32(2)).reveal())
This will output 5.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbitfix(**kwargs)[source]¶
Secret signed fixed-point number in one binary register. Use
set_precision()to change the precision.This class is retained for compatibility, but development now focuses on
sbitfixvec.Example:
print_ln('add: %s', (sbitfix(0.5) + sbitfix(0.3)).reveal()) print_ln('mul: %s', (sbitfix(0.5) * sbitfix(0.3)).reveal()) print_ln('sub: %s', (sbitfix(0.5) - sbitfix(0.3)).reveal()) print_ln('lt: %s', (sbitfix(0.5) < sbitfix(0.3)).reveal())
will output roughly:
add: 0.800003 mul: 0.149994 sub: 0.199997 lt: 0
Note that the default precision (16 bits after the dot, 31 bits in total) only allows numbers up to \(2^{31-16-1} \approx 16000\). You can increase this using
set_precision().- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- add(*args, **kwargs)¶
Secret fixed-point addition.
- Parameters
other – sfix/cfix/sint/cint/regint/int
- bit_decompose(n_bits=None)¶
Bit decomposition.
- compute_reciprocal(*args, **kwargs)¶
Secret fixed-point reciprocal.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- reveal()¶
Reveal secret fixed-point number.
- Returns
relevant clear type
- classmethod set_precision(f, k=None)[source]¶
Set the precision of the integer representation. The initial defaults are chosen to allow the best optimization of probabilistic truncation in computation modulo 2^64 (2*k < 64). Generally, 2*k must be at most the integer length for rings and at most m-s-1 for computation modulo an m-bit prime and statistical security s (default 40).
- Parameters
f – bit length of decimal part (initial default 16)
k – whole bit length of fixed point, defaults to twice
fif not given (initial default 31)
- square()¶
Square.
- store_in_mem(address)¶
Store in memory by public address.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbitfixvec(value=None, *args, **kwargs)[source]¶
Vector of fixed-point numbers for parallel binary computation.
Use
set_precision()to change the precision.Example:
a = sbitfixvec([sbitfix(0.3), sbitfix(0.5)]) b = sbitfixvec([sbitfix(0.4), sbitfix(0.6)]) c = (a + b).elements() print_ln('add: %s, %s', c[0].reveal(), c[1].reveal()) c = (a * b).elements() print_ln('mul: %s, %s', c[0].reveal(), c[1].reveal()) c = (a - b).elements() print_ln('sub: %s, %s', c[0].reveal(), c[1].reveal()) c = (a < b).elements() print_ln('lt: %s, %s', c[0].reveal(), c[1].reveal())
This should output roughly:
add: 0.699997, 1.10001 mul: 0.119995, 0.300003 sub: -0.0999908, -0.100021 lt: 1, 1
- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- add(*args, **kwargs)¶
Secret fixed-point addition.
- Parameters
other – sfix/cfix/sint/cint/regint/int
- bit_decompose(n_bits=None)¶
Bit decomposition.
- compute_reciprocal(*args, **kwargs)¶
Secret fixed-point reciprocal.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- reveal()¶
Reveal secret fixed-point number.
- Returns
relevant clear type
- classmethod set_precision(f, k=None)[source]¶
Set the precision of the integer representation. The initial defaults are chosen to allow the best optimization of probabilistic truncation in computation modulo 2^64 (2*k < 64). Generally, 2*k must be at most the integer length for rings and at most m-s-1 for computation modulo an m-bit prime and statistical security s (default 40).
- Parameters
f – bit length of decimal part (initial default 16)
k – whole bit length of fixed point, defaults to twice
fif not given (initial default 31)
- square()¶
Square.
- store_in_mem(address)¶
Store in memory by public address.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbitint(*args, **kwargs)[source]¶
Secret signed integer in one binary register. Use
get_type()to specify the bit length:si32 = sbitint.get_type(32) print_ln('add: %s', (si32(5) + si32(3)).reveal()) print_ln('sub: %s', (si32(5) - si32(3)).reveal()) print_ln('mul: %s', (si32(5) * si32(3)).reveal()) print_ln('lt: %s', (si32(5) < si32(3)).reveal())
This should output:
add: 8 sub: 2 mul: 15 lt: 0
This class is retained for compatibility, but development now focuses on
sbitintvec.- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- classmethod bit_adder(a, b, carry_in=0, get_carry=False)¶
Binary adder in binary circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod get_input_from(player, n_bits=None)¶
Secret input from
player.- Param
player (int)
- classmethod get_type(n, other=None)[source]¶
Returns a signed integer type with fixed length.
- Parameters
n – length
- static half_adder(a, b)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(x, y)¶
Vectorized oblivious selection:
sb32 = sbits.get_type(32) print_ln('%s', sb32(3).if_else(sb32(5), sb32(2)).reveal())
This will output 1.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- square()¶
Square.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbitintvec(elements=None, length=None, input_length=None)[source]¶
Vector of signed integers for parallel binary computation. The following example uses vectors of size two:
sb32 = sbits.get_type(32) siv32 = sbitintvec.get_type(32) a = siv32([sb32(3), sb32(5)]) b = siv32([sb32(4), sb32(6)]) c = (a + b).elements() print_ln('add: %s, %s', c[0].reveal(), c[1].reveal()) c = (a * b).elements() print_ln('mul: %s, %s', c[0].reveal(), c[1].reveal()) c = (a - b).elements() print_ln('sub: %s, %s', c[0].reveal(), c[1].reveal()) c = (a < b).elements() print_ln('lt: %s, %s', c[0].reveal(), c[1].reveal())
This should output:
add: 7, 11 mul: 12, 30 sub: -1, 11 lt: 1, 1
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod from_hex(string)¶
Create from hexadecimal string (little-endian).
- classmethod get_type(n)¶
Create type for fixed-length vector of registers of secret bits.
As with
sbitvec, you can access the rows by membervand the columns by callingelements.
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- iadd(other)¶
Addition assignment. This uses
update()internally.
- max(other)¶
Maximum.
- Parameters
other – any compatible type
- min(other)¶
Minimum.
- Parameters
other – any compatible type
- popcnt()¶
Population count / Hamming weight.
- Returns
sbitintvecof required length
- reveal_print_hex()¶
Reveal and print in hexademical (one line per element).
- square()¶
Square.
- class Compiler.GC.types.sbits(*args, **kwargs)[source]¶
Secret bits register. This type supports basic bit-wise operations:
sb32 = sbits.get_type(32) a = sb32(3) b = sb32(5) print_ln('XOR: %s', (a ^ b).reveal()) print_ln('AND: %s', (a & b).reveal()) print_ln('NOT: %s', (~a).reveal())
This will output the following:
XOR: 6 AND: 1 NOT: -4
Instances can be also be initalized from
regintandsint.- classmethod Array(size, *args, **kwargs)¶
Type-dependent array. Example:
a = sint.Array(10)
- static bit_adder(*args, **kwargs)[source]¶
Binary adder in binary circuits.
- Parameters
a – summand (list of 0/1 in compatible type)
b – summand (list of 0/1 in compatible type)
carry_in – input carry (default 0)
get_carry – add final carry to output
- Returns
list of 0/1 in relevant type
- bit_and(other)¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod get_input_from(player, n_bits=None)[source]¶
Secret input from
player.- Param
player (int)
- classmethod get_type(length)¶
Returns a fixed-length type.
- half_adder(other)¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- if_else(x, y)¶
Vectorized oblivious selection:
sb32 = sbits.get_type(32) print_ln('%s', sb32(3).if_else(sb32(5), sb32(2)).reveal())
This will output 1.
- update(other)¶
Update register. Useful in loops like
for_range().- Parameters
other – any convertible type
- class Compiler.GC.types.sbitvec(elements=None, length=None, input_length=None)[source]¶
Vector of registers of secret bits, effectively a matrix of secret bits. This facilitates parallel arithmetic operations in binary circuits. Container types are not supported, use
sbitvec.get_typefor that.You can access the rows by member
vand the columns by callingelements.There are four ways to create an instance:
By transposition:
sb32 = sbits.get_type(32) x = sbitvec([sb32(5), sb32(3), sb32(0)]) print_ln('%s', [x.v[0].reveal(), x.v[1].reveal(), x.v[2].reveal()]) print_ln('%s', [x.elements()[0].reveal(), x.elements()[1].reveal()])
This should output:
[3, 2, 1] [5, 3]
Without transposition:
sb32 = sbits.get_type(32) x = sbitvec.from_vec([sb32(5), sb32(3)]) print_ln('%s', [x.v[0].reveal(), x.v[1].reveal()])
This should output:
[5, 3]
From
sint:y = sint(5) x = sbitvec(y, 3, 3) print_ln('%s', [x.v[0].reveal(), x.v[1].reveal(), x.v[2].reveal()])
This should output:
[1, 0, 1]
Private input:
x = sbitvec.get_type(32).get_input_from(player)
- bit_and(other)[source]¶
AND in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- bit_not()¶
NOT in binary circuits.
- bit_or(other)¶
OR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
type depends on inputs (secret if any of them is)
- bit_xor(other)[source]¶
XOR in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Return type
depending on inputs (secret if any of them is)
- classmethod get_type(n)[source]¶
Create type for fixed-length vector of registers of secret bits.
As with
sbitvec, you can access the rows by membervand the columns by callingelements.
- half_adder(other)[source]¶
Half adder in binary circuits.
- Parameters
self/other – 0 or 1 (any compatible type)
- Returns
binary sum, carry
- Return type
depending on inputs (secret if any of them is)
- popcnt()[source]¶
Population count / Hamming weight.
- Returns
sbitintvecof required length
Compiler.library module¶
This module defines functions directly available in high-level programs, in particularly providing flow control and output.
- Compiler.library.accept_client_connection(port)[source]¶
Accept client connection on specific port base.
- Parameters
port – port base (int/regint/cint)
- Returns
client id
- Compiler.library.break_point(name='')[source]¶
Insert break point. This makes sure that all following code will be executed after preceding code.
- Parameters
name – Name for identification (optional)
- Compiler.library.check_point()[source]¶
Force MAC checks in current thread and all idle threads if the current thread is the main thread. This implies a break point.
- Compiler.library.crash(condition=None)[source]¶
Crash virtual machine.
- Parameters
condition – crash if true (default: true)
- Compiler.library.do_while(loop_fn, g=None)[source]¶
Do-while loop. The loop is stopped if the return value is zero. It must be public. The following executes exactly once:
@do_while def _(): ... return regint(0)
- Compiler.library.for_range(start, stop=None, step=None)[source]¶
Decorator to execute loop bodies consecutively. Arguments work as in Python
range(), but they can be any public integer. Information has to be passed out via container types such asArrayor usingupdate(). Note that changing Python data structures such as lists within the loop is not possible, but the compiler cannot warn about this.- Parameters
start/stop/step – regint/cint/int
The following should output 10:
n = 10 a = sint.Array(n) x = sint(0) @for_range(n) def _(i): a[i] = i x.update(x + 1) print_ln('%s', x.reveal())
- Compiler.library.for_range_multithread(n_threads, n_parallel, n_loops, thread_mem_req={}, budget=None)[source]¶
Execute
n_loopsloop bodies in up ton_threadsthreads, up ton_parallelin parallel per thread.- Parameters
n_threads/n_parallel – compile-time (int)
n_loops – regint/cint/int
- Compiler.library.for_range_opt(start, stop=None, step=None, budget=None)[source]¶
Execute loop bodies in parallel up to an optimization budget. This prevents excessive loop unrolling. The budget is respected even with nested loops. Note that the optimization is rather rudimentary for runtime
n_loops(regint/cint). Consider usingfor_range_parallel()in this case. Using further control flow constructions inside other thanfor_range_opt()(e.g,for_range()) breaks the optimization.- Parameters
start/stop/step – int/regint/cint (used as in
range()) orstartonly as list/tuple of int (see below)budget – number of instructions after which to start optimization (default is 100,000)
Example:
@for_range_opt(n) def _(i): ...
Multidimensional ranges are supported as well. The following executes
f(0, 0)tof(4, 2)in parallel according to the budget.@for_range_opt([5, 3]) def f(i, j): ...
- Compiler.library.for_range_opt_multithread(n_threads, n_loops, budget=None)[source]¶
Execute
n_loopsloop bodies in up ton_threadsthreads, in parallel up to an optimization budget per thread similar tofor_range_opt(). Note that optimization is rather rudimentary for runtimen_loops(regint/cint). Consider usingfor_range_multithread()in this case.- Parameters
n_threads – compile-time (int)
n_loops – regint/cint/int
The following will execute loop bodies 0-9 in one thread, 10-19 in another etc:
@for_range_opt_multithread(8, 80) def _(i): ...
Multidimensional ranges are supported as well. The following executes
f(0, 0)tof(2, 0)in one thread andf(2, 1)tof(4, 2)in another.@for_range_opt_multithread(2, [5, 3]) def f(i, j): ...
Note that you cannot use registers across threads. Use
MemValueinstead:a = MemValue(sint(0)) @for_range_opt_multithread(8, 80) def _(i): b = a + 1
- Compiler.library.for_range_parallel(n_parallel, n_loops)[source]¶
Decorator to execute a loop
n_loopsup ton_parallelloop bodies with optimized communication in a single thread. In most cases, it is easier to usefor_range_opt(). Using any other control flow instruction inside the loop breaks the optimization.- Parameters
n_parallel – optimization parameter (int)
n_loops – regint/cint/int or list of int
Example:
@for_range_parallel(n_parallel, n_loops) def _(i): a[i] = a[i] * a[i]
Multidimensional ranges are supported as well. The following executes
f(0, 0)tof(4, 2), two calls in parallel.@for_range_parallel(2, [5, 3]) def f(i, j): ...
- Compiler.library.foreach_enumerate(a)[source]¶
Run-time loop over public data. This uses
Player-Data/Public-Input/<progname>. Example:@foreach_enumerate([2, 8, 3]) def _(i, j): print_ln('%s: %s', i, j)
This will output:
0: 2 1: 8 2: 3
- Compiler.library.get_player_id()[source]¶
- Returns
player number
- Return type
localint (cannot be used for computation)
- Compiler.library.get_threshold()[source]¶
The threshold is the maximal number of corrupted players.
- Return type
- Compiler.library.if_(condition)[source]¶
Conditional execution without else block.
- Parameters
condition – regint/cint/int
Usage:
@if_(x > 0) def _(): ...
- Compiler.library.if_e(condition)[source]¶
Conditional execution with else block. Use
MemValueto assign values that live beyond.- Parameters
condition – regint/cint/int
Usage:
y = MemValue(0) @if_e(x > 0) def _(): y.write(1) @else_ def _(): y.write(0)
- Compiler.library.init_client_connection(host, port, my_id, relative_port=True)[source]¶
Initiate connection to another party as client.
- Parameters
host – hostname
port – port base (int/regint/cint)
my_id – client id to use
relative_port – whether to add party number to port number
- Returns
connection id
- Compiler.library.listen_for_clients(port)[source]¶
Listen for clients on specific port base.
- Parameters
port – port base (int/regint/cint)
- Compiler.library.map_sum_opt(n_threads, n_loops, types)[source]¶
Multi-threaded sum reduction. The following computes a sum of ten squares in three threads:
@map_sum_opt(3, 10, [sint]) def summer(i): return sint(i) ** 2 result = summer()
- Parameters
n_threads – number of threads (int)
n_loops – number of loop runs (regint/cint/int)
types – return type, must match the return statement in the loop
- Compiler.library.map_sum_simple(n_threads, n_loops, type, size)[source]¶
Vectorized multi-threaded sum reduction. The following computes a 100 sums of ten squares in three threads:
@map_sum_simple(3, 10, sint, 100) def summer(i): return sint(regint.inc(100, i, 0)) ** 2 result = summer()
- Parameters
n_threads – number of threads (int)
n_loops – number of loop runs (regint/cint/int)
type – return type, must match the return statement in the loop
size – vector size, must match the return statement in the loop
- Compiler.library.multithread(n_threads, n_items=None, max_size=None)[source]¶
Distribute the computation of
n_itemston_threadsthreads, but leave the in-thread repetition up to the user.- Parameters
n_threads – compile-time (int)
n_items – regint/cint/int (default:
n_threads)max_size – maximum size to be processed at once (default: no limit)
The following executes
f(0, 8),f(8, 8), andf(16, 9)in three different threads:@multithread(8, 25) def f(base, size): ...
- Compiler.library.print_float_precision(n)[source]¶
Set the precision for floating-point printing.
- Parameters
n – number of digits (int)
- Compiler.library.print_ln(s='', *args, **kwargs)[source]¶
Print line, with optional args for adding variables/registers with
%s. By default only player 0 outputs, but the-Icommand-line option changes that.- Parameters
s – Python string with same number of
%sas length ofargsargs – list of public values (regint/cint/int/cfix/cfloat/localint)
print_secrets – whether to output secret shares
Example:
print_ln('a is %s.', a.reveal())
- Compiler.library.print_ln_if(cond, ss, *args)[source]¶
Print line if
condis true. The further arguments are treated as inprint_str()/print_ln().- Parameters
cond – regint/cint/int/localint
ss – Python string
args – list of public values
Example:
print_ln_if(get_player_id() == 0, 'Player 0 here')
- Compiler.library.print_ln_to(player, ss, *args)[source]¶
Print line at
playeronly. Note that printing is disabled by default except at player 0. Activate interactive mode with -I or use -OF . to enable it for all players.- Parameters
player – int
ss – Python string
args – list of values known to
player
Example:
print_ln_to(player, 'output for %s: %s', player, x.reveal_to(player))
- Compiler.library.print_str(s, *args, print_secrets=False)[source]¶
Print a string, with optional args for adding variables/registers with
%s.- Parameters
s – format string
args – arguments (any type)
print_secrets – whether to output secret shares
- Compiler.library.print_str_if(cond, ss, *args)[source]¶
Print string conditionally. See
print_ln_if()for details.
- Compiler.library.runtime_error(msg='', *args)[source]¶
Print an error message and abort the runtime. Parameters work as in
print_ln()
- Compiler.library.runtime_error_if(condition, msg='', *args)[source]¶
Conditionally print an error message and abort the runtime.
- Parameters
condition – regint/cint/int/cbit
msg – message
args – list of public values to fit
%sin the message
- Compiler.library.start_timer(timer_id=0)[source]¶
Start timer. Timer 0 runs from the start of the program. The total time of all used timers is output at the end. Fails if already running.
- Parameters
timer_id – compile-time (int)
- Compiler.library.stop_timer(timer_id=0)[source]¶
Stop timer. Fails if not running.
- Parameters
timer_id – compile-time (int)
- Compiler.library.tree_reduce(function, sequence)[source]¶
Round-efficient reduction. The following computes the maximum of the list
l:m = tree_reduce(lambda x, y: x.max(y), l)
- Parameters
function – reduction function taking two arguments
sequence – list, vector, or array
- Compiler.library.tree_reduce_multithread(n_threads, function, vector)[source]¶
Round-efficient reduction in several threads. The following code computes the maximum of an array in 10 threads:
tree_reduce_multithread(10, lambda x, y: x.max(y), a)
- Parameters
n_threads – number of threads (int)
function – reduction function taking exactly two arguments
vector – register vector or array
Compiler.mpc_math module¶
Module for math operations.
Implements trigonometric and logarithmic functions.
This has to imported explicitly.
- Compiler.mpc_math.atan(*args, **kwargs)¶
Returns the arctangent (sfix) of any given fractional value.
- Parameters
x – fractional input (sfix).
- Returns
arctan of
x(sfix).
- Compiler.mpc_math.acos(x)[source]¶
Returns the arccosine (sfix) of any given fractional value.
- Parameters
x – fractional input (sfix). \(-1 \le x \le 1\)
- Returns
arccos of
x(sfix).
- Compiler.mpc_math.asin(x)[source]¶
Returns the arcsine (sfix) of any given fractional value.
- Parameters
x – fractional input (sfix). valid interval is \(-1 \le x \le 1\)
- Returns
arcsin of
x(sfix).
- Compiler.mpc_math.cos(*args, **kwargs)¶
Returns the cosine of any given fractional value.
- Parameters
x – fractional input (sfix, sfloat)
- Returns
cos of
x(sfix, sfloat)
- Compiler.mpc_math.exp2_fx(self, *args, **kwargs)¶
Power of two for fixed-point numbers.
- Parameters
a – exponent for \(2^a\) (sfix)
zero_output – whether to output zero for very small values. If not, the result will be undefined.
- Returns
\(2^a\) if it is within the range. Undefined otherwise
- Compiler.mpc_math.InvertSqrt(self, *args, **kwargs)¶
Reciprocal square root approximation by Lu et al.
- Compiler.mpc_math.log2_fx(self, *args, **kwargs)¶
Returns the result of \(\log_2(x)\) for any unbounded number. This is achieved by changing
xinto \(f \cdot 2^n\) where f is bounded by \([0.5, 1]\). Then the polynomials are used to calculate \(\log_2(f)\), which is then just added to \(n\).- Parameters
x – input for \(\log_2\) (sfix, sint).
- Returns
(sfix) the value of \(\log_2(x)\)
- Compiler.mpc_math.log_fx(x, b)[source]¶
Returns the value of the expression \(\log_b(x)\) where
xis secret shared. It useslog2_fx()to calculate the expression \(\log_b(2) \cdot \log_2(x)\).- Parameters
x – (sfix, sint) secret shared coefficient for log.
b – (float) base for log operation.
- Returns
(sfix) the value of \(log_b(x)\).
- Compiler.mpc_math.pow_fx(x, y)[source]¶
Returns the value of the expression \(x^y\) where both inputs are secret shared. It uses
log2_fx()together withexp2_fx()to calculate the expression \(2^{y \log_2(x)}\).- Parameters
x – (sfix) secret shared base.
y – (sfix, clear types) secret shared exponent.
- Returns
\(x^y\) (sfix) if positive and in range
- Compiler.mpc_math.sin(*args, **kwargs)¶
Returns the sine of any given fractional value.
- Parameters
x – fractional input (sfix, sfloat)
- Returns
sin of
x(sfix, sfloat)
- Compiler.mpc_math.sqrt(self, *args, **kwargs)¶
Square root.
- Parameters
x – fractional input (sfix).
- Returns
square root of
x(sfix).
- Compiler.mpc_math.tan(*args, **kwargs)¶
Returns the tangent of any given fractional value.
- Parameters
x – fractional input (sfix, sfloat)
- Returns
tan of
x(sfix, sfloat)
Compiler.ml module¶
This module contains machine learning functionality. It is work in progress, so you must expect things to change. The only tested functionality for training is using consecutive layers. This includes logistic regression. It can be run as follows:
sgd = ml.SGD([ml.Dense(n_examples, n_features, 1),
ml.Output(n_examples, approx=True)], n_epochs,
report_loss=True)
sgd.layers[0].X.input_from(0)
sgd.layers[1].Y.input_from(1)
sgd.reset()
sgd.run()
This loads measurements from party 0 and labels (0/1) from party
1. After running, the model is stored in sgd.layers[0].W and
sgd.layers[0].b. The approx parameter determines
whether to use an approximate sigmoid function. Setting it to 5 uses
a five-piece approximation instead of a three-piece one.
A simple network for MNIST using two dense layers can be trained as follows:
sgd = ml.SGD([ml.Dense(60000, 784, 128, activation='relu'),
ml.Dense(60000, 128, 10),
ml.MultiOutput(60000, 10)], n_epochs,
report_loss=True)
sgd.layers[0].X.input_from(0)
sgd.layers[1].Y.input_from(1)
sgd.reset()
sgd.run()
See this repository for scripts importing MNIST training data and further examples.
Inference can be run as follows:
data = sfix.Matrix(n_test, n_features)
data.input_from(0)
res = sgd.eval(data)
print_ln('Results: %s', [x.reveal() for x in res])
For inference/classification, this module offers the layers necessary for neural networks such as DenseNet, ResNet, and SqueezeNet. A minimal example using input from player 0 and model from player 1 looks as follows:
graph = Optimizer()
graph.layers = layers
layers[0].X.input_from(0)
for layer in layers:
layer.input_from(1)
graph.forward(1)
res = layers[-1].Y
See the readme for an example of how to run MP-SPDZ on TensorFlow graphs.
- class Compiler.ml.Adam(layers, n_epochs=1, approx=False, amsgrad=False, normalize=False)[source]¶
Bases:
Compiler.ml.OptimizerAdam/AMSgrad optimizer.
- Parameters
layers – layers of linear graph
approx – use approximation for inverse square root (bool)
amsgrad – use AMSgrad (bool)
- backward(**kwargs)¶
Compute backward propagation.
- eval(**kwargs)¶
Compute evaluation after training.
- Parameters
data – sample data (
Compiler.types.Matrixwith one row per sample)top – return top prediction instead of probability distribution
- Returns
sfix/sint Array (depening on
top)
- fit(X, Y, epochs=1, batch_size=128, validation_data=(None, None), program=None, reset=True, print_accuracy=False, print_loss=False)¶
Train model.
- Parameters
X – training sample data (sfix tensor)
Y – training labels (sint/sfix tensor)
epochs – number of epochs (int)
batch_size – batch size (int)
validation_data – tuple of test sample data and labels for accuracy testing (optional; reveals labels)
program –
Programinstance to use command-line parameters (optional)reset – whether to initialize model
print_accuracy – print accuracy on training data (reveals labels)
print_loss – reveal and print training loss after every batch
- forward(**kwargs)¶
Compute graph.
- Parameters
N – batch size (used if batch not given)
batch – indices for computation (
Arrayor list)keep_intermediate – do not free memory of intermediate results after use
- property layers¶
Get all layers.
- reset()¶
Initialize weights.
- reveal_correctness(data, truth, batch_size=128, running=False)¶
Test correctness by revealing results.
- Parameters
data – test sample data
truth – test labels
batch_size – batch size
running – output after every batch
- run(**kwargs)¶
Run training.
- Parameters
batch_size – batch size (defaults to example size of first layer)
stop_on_loss – stop when loss falls below this (default: 0)
- set_layers_with_inputs(layers)¶
Construct graph from
inputsmembers of list of layers.
- class Compiler.ml.Add(inputs)[source]¶
Bases:
Compiler.ml.NoVariableLayerFixed-point addition layer.
- Parameters
inputs – two input layers with same shape (tuple/list)
- class Compiler.ml.Argmax(shape)[source]¶
Bases:
Compiler.ml.NoVariableLayerFixed-point Argmax layer.
- Parameters
shape – input shape (tuple/list of two int)
- class Compiler.ml.BatchNorm(shape, approx=True, args=None)[source]¶
Bases:
Compiler.ml.LayerFixed-point batch normalization layer.
- Parameters
shape – input/output shape (tuple/list of four int)
approx – use approximate square root
- class Compiler.ml.Concat(inputs, dimension)[source]¶
Bases:
Compiler.ml.NoVariableLayerFixed-point concatentation layer.
- Parameters
inputs – two input layers (tuple/list)
dimension – dimension for concatenation (must be 3)
- class Compiler.ml.Dense(N, d_in, d_out, d=1, activation='id', debug=False)[source]¶
Bases:
Compiler.ml.DenseBaseFixed-point dense (matrix multiplication) layer.
- Parameters
N – number of examples
d_in – input dimension
d_out – output dimension
- class Compiler.ml.Dropout(N, d1, d2=1, alpha=0.5)[source]¶
Bases:
Compiler.ml.NoVariableLayerDropout layer.
- Parameters
N – number of examples
d1 – total dimension
alpha – probability (power of two)
- class Compiler.ml.FixAveragePool2d(input_shape, output_shape, filter_size, strides=(1, 1), padding=0)[source]¶
Bases:
Compiler.ml.PoolBase,Compiler.ml.FixBaseFixed-point 2D AvgPool layer.
- Parameters
input_shape – input shape (tuple/list of four int)
output_shape – output shape (tuple/list of four int)
filter_size – filter size (int or tuple/list of two int)
strides – strides (int or tuple/list of two int)
padding –
'SAME','VALID', int, or tuple/list of two int
- class Compiler.ml.FixConv2d(input_shape, weight_shape, bias_shape, output_shape, stride, padding='SAME', tf_weight_format=False, inputs=None)[source]¶
Bases:
Compiler.ml.Conv2d,Compiler.ml.FixBaseFixed-point 2D convolution layer.
- Parameters
input_shape – input shape (tuple/list of four int)
weight_shape – weight shape (tuple/list of four int)
bias_shape – bias shape (tuple/list of one int)
output_shape – output shape (tuple/list of four int)
stride – stride (tuple/list of two int)
padding –
'SAME'(default),'VALID', or tuple/list of two inttf_weight_format – weight shape format is (height, width, input channels, output channels) instead of the default (output channels, height, width, input channels)
- class Compiler.ml.FusedBatchNorm(shape, inputs=None)[source]¶
Bases:
Compiler.ml.LayerFixed-point fused batch normalization layer (inference only).
- Parameters
shape – input/output shape (tuple/list of four int)
- class Compiler.ml.MaxPool(shape, strides=(1, 2, 2, 1), ksize=(1, 2, 2, 1), padding='VALID')[source]¶
Bases:
Compiler.ml.PoolBaseFixed-point MaxPool layer.
- Parameters
shape – input shape (tuple/list of four int)
strides – strides (tuple/list of four int, first and last must be 1)
ksize – kernel size (tuple/list of four int, first and last must be 1)
padding –
'VALID'(default),'SAME', integer, or list/tuple of integers
- class Compiler.ml.MultiOutput(N, d_out, approx=False, debug=False)[source]¶
Bases:
Compiler.ml.MultiOutputBaseOutput layer for multi-class classification with softmax and cross entropy.
- Parameters
N – number of examples
d_out – number of classes
approx – use ReLU division instead of softmax for the loss
- class Compiler.ml.Optimizer(layers=[], report_loss=None)[source]¶
Bases:
objectBase class for graphs of layers.
- eval(**kwargs)[source]¶
Compute evaluation after training.
- Parameters
data – sample data (
Compiler.types.Matrixwith one row per sample)top – return top prediction instead of probability distribution
- Returns
sfix/sint Array (depening on
top)
- fit(X, Y, epochs=1, batch_size=128, validation_data=(None, None), program=None, reset=True, print_accuracy=False, print_loss=False)[source]¶
Train model.
- Parameters
X – training sample data (sfix tensor)
Y – training labels (sint/sfix tensor)
epochs – number of epochs (int)
batch_size – batch size (int)
validation_data – tuple of test sample data and labels for accuracy testing (optional; reveals labels)
program –
Programinstance to use command-line parameters (optional)reset – whether to initialize model
print_accuracy – print accuracy on training data (reveals labels)
print_loss – reveal and print training loss after every batch
- forward(**kwargs)[source]¶
Compute graph.
- Parameters
N – batch size (used if batch not given)
batch – indices for computation (
Arrayor list)keep_intermediate – do not free memory of intermediate results after use
- property layers¶
Get all layers.
- reveal_correctness(data, truth, batch_size=128, running=False)[source]¶
Test correctness by revealing results.
- Parameters
data – test sample data
truth – test labels
batch_size – batch size
running – output after every batch
- class Compiler.ml.Output(N, debug=False, approx=False)[source]¶
Bases:
Compiler.ml.NoVariableLayerFixed-point logistic regression output layer.
- Parameters
N – number of examples
approx –
False(default) or parameter forapprox_sigmoid
- class Compiler.ml.Relu(shape, inputs=None)[source]¶
Bases:
Compiler.ml.ElementWiseLayerFixed-point ReLU layer.
- Parameters
shape – input/output shape (tuple/list of int)
- prime_type¶
alias of
Compiler.types.sint
- class Compiler.ml.ReluMultiOutput(N, d_out, approx=False, debug=False)[source]¶
Bases:
Compiler.ml.MultiOutputBaseOutput layer for multi-class classification with back-propagation based on ReLU division.
- Parameters
N – number of examples
d_out – number of classes
- class Compiler.ml.SGD(layers, n_epochs=1, debug=False, report_loss=None)[source]¶
Bases:
Compiler.ml.OptimizerStochastic gradient descent.
- Parameters
layers – layers of linear graph
n_epochs – number of epochs for training
report_loss – disclose and print loss
- backward(**kwargs)¶
Compute backward propagation.
- eval(**kwargs)¶
Compute evaluation after training.
- Parameters
data – sample data (
Compiler.types.Matrixwith one row per sample)top – return top prediction instead of probability distribution
- Returns
sfix/sint Array (depening on
top)
- fit(X, Y, epochs=1, batch_size=128, validation_data=(None, None), program=None, reset=True, print_accuracy=False, print_loss=False)¶
Train model.
- Parameters
X – training sample data (sfix tensor)
Y – training labels (sint/sfix tensor)
epochs – number of epochs (int)
batch_size – batch size (int)
validation_data – tuple of test sample data and labels for accuracy testing (optional; reveals labels)
program –
Programinstance to use command-line parameters (optional)reset – whether to initialize model
print_accuracy – print accuracy on training data (reveals labels)
print_loss – reveal and print training loss after every batch
- forward(**kwargs)¶
Compute graph.
- Parameters
N – batch size (used if batch not given)
batch – indices for computation (
Arrayor list)keep_intermediate – do not free memory of intermediate results after use
- property layers¶
Get all layers.
- reset(**kwargs)[source]¶
Reset layer parameters.
- Parameters
X_by_label – if given, set training data by public labels for balancing
- reveal_correctness(data, truth, batch_size=128, running=False)¶
Test correctness by revealing results.
- Parameters
data – test sample data
truth – test labels
batch_size – batch size
running – output after every batch
- run(**kwargs)¶
Run training.
- Parameters
batch_size – batch size (defaults to example size of first layer)
stop_on_loss – stop when loss falls below this (default: 0)
- set_layers_with_inputs(layers)¶
Construct graph from
inputsmembers of list of layers.
- class Compiler.ml.SGDLinear(n_epochs=1, batch_size=1, program=None)[source]¶
Bases:
Compiler.ml.OneLayerSGDLinear regression using SGD.
- Parameters
n_epochs – number of epochs
batch_size – batch size
program – program object to use command-line options from (default is not to use any)
- fit(X_train, y_train)¶
Train classifier.
- Parameters
X_train – training data (sfix matrix)
y_train – training binary labels (sint/sfix array)
- fit_with_testing(X_train, y_train, X_test, y_test)¶
Train classifier with accuracy output after every epoch. This reveals all labels to simplify the accuracy computation.
- Parameters
X_train – training data (sfix matrix)
y_train – training labels (sint/sfix array)
X_test – testing data (sfix matrix)
y_test – testing labels (sint/sfix array)
- predict(X)¶
Use model for prediction.
- Parameters
X – sample data with row-wise samples (sfix matrix)
- Returns
sfix array
- class Compiler.ml.SGDLogistic(n_epochs=1, batch_size=1, program=None)[source]¶
Bases:
Compiler.ml.OneLayerSGDLogistic regression using SGD.
- Parameters
n_epochs – number of epochs
batch_size – batch size
program – program object to use command-line options from (default is not to use any)
- fit(X_train, y_train)¶
Train classifier.
- Parameters
X_train – training data (sfix matrix)
y_train – training binary labels (sint/sfix array)
- fit_with_testing(X_train, y_train, X_test, y_test)¶
Train classifier with accuracy output after every epoch. This reveals all labels to simplify the accuracy computation.
- Parameters
X_train – training data (sfix matrix)
y_train – training labels (sint/sfix array)
X_test – testing data (sfix matrix)
y_test – testing labels (sint/sfix array)
- class Compiler.ml.Square(shape, inputs=None)[source]¶
Bases:
Compiler.ml.ElementWiseLayerFixed-point square layer.
- Parameters
shape – input/output shape (tuple/list of int)
- prime_type¶
alias of
Compiler.types.sfix
- Compiler.ml.argmax(x)[source]¶
Compute index of maximum element.
- Parameters
x – iterable
- Returns
sint or 0 if
xhas length 1
- Compiler.ml.cholesky(A, reveal_diagonal=False)[source]¶
Cholesky decomposition.
- Returns
lower triangular matrix
- Compiler.ml.easyConv2d(input_shape, batch_size, out_channels, kernel_size, stride=1, padding=0)[source]¶
More convenient interface to
FixConv2d.- Parameters
input_shape – input shape (tuple/list of four int)
out_channels – output channels (int)
kernel_size – kernel size (int or tuple/list of two int)
stride – stride (int or tuple/list of two int)
padding –
'SAME','VALID', int, or tuple/list of two int
- Compiler.ml.easyMaxPool(input_shape, kernel_size, stride=None, padding=0)[source]¶
More convenient interface to
MaxPool.- Parameters
input_shape – input shape (tuple/list of four int)
kernel_size – kernel size (int or tuple/list of two int)
stride – stride (int or tuple/list of two int)
padding –
'SAME','VALID', int, or tuple/list of two int
- Compiler.ml.layers_from_torch(sequence, data_input_shape, batch_size, input_via=None, regression=False)[source]¶
Convert a PyTorch Sequential object to MP-SPDZ layers.
- Parameters
sequence – PyTorch Sequential object
data_input_shape – input shape (list of four int)
batch_size – batch size (int)
input_via – player to input model data via (default: don’t)
regression – regression (default: classification)
- Compiler.ml.mr(A, n_iterations, stop=False)[source]¶
Iterative matrix inverse approximation.
- Parameters
A – matrix to invert
n_iterations – maximum number of iterations
stop – whether to stop when converged (implies revealing)
- Compiler.ml.solve_linear(A, b, n_iterations, progress=False, n_threads=None, stop=False, already_symmetric=False, precond=False)[source]¶
Iterative linear solution approximation for \(Ax=b\).
- Parameters
progress – print some information on the progress (implies revealing)
n_threads – number of threads to use
stop – whether to stop when converged (implies revealing)
- Compiler.ml.approx_sigmoid(*args, **kwargs)¶
Piece-wise approximate sigmoid as in Hong et al.
- Parameters
x – input
n – number of pieces, 3 (default) or 5
Compiler.decision_tree module¶
- class Compiler.decision_tree.TreeClassifier(max_depth, n_threads=None)[source]¶
Tree classification with convenient interface. Uses
TreeTrainerinternally.- Parameters
max_depth – the depth of the decision tree
n_threads – number of threads used in training
- fit(X, y, attr_types=None)[source]¶
Train tree.
- Parameters
X – sample data with row-wise samples (sint/sfix matrix)
y – binary labels (sint list/array)
- fit_with_testing(X_train, y_train, X_test, y_test, attr_types=None, output_trees=False, debug=False)[source]¶
Train tree with accuracy output after every level.
- Parameters
X_train – training data with row-wise samples (sint/sfix matrix)
y_train – training binary labels (sint list/array)
X_test – testing data with row-wise samples (sint/sfix matrix)
y_test – testing binary labels (sint list/array)
attr_types – attributes types (list of ‘b’/’c’ for binary/continuous; default is all continuous)
output_trees – output tree after every level
debug – output debugging information
- class Compiler.decision_tree.TreeTrainer(x, y, h, binary=False, attr_lengths=None, n_threads=None)[source]¶
Decision tree training by Hamada et al.
- Parameters
x – sample data (by attribute, list or
Matrix)y – binary labels (list or sint vector)
h – height (int)
binary – binary attributes instead of continuous
attr_lengths – attribute description for mixed data (list of 0/1 for continuous/binary)
n_threads – number of threads (default: single thread)
- Compiler.decision_tree.output_decision_tree(layers)[source]¶
Print decision tree output by
TreeTrainer.
- Compiler.decision_tree.preprocess_pandas(data)[source]¶
Preprocess pandas data frame to suit
TreeClassifierby expanding non-continuous attributes to several binary attributes as a unary encoding.- Returns
a tuple of the processed data and a type list for the
attr_typesargument.
- Compiler.decision_tree.run_decision_tree(layers, data)[source]¶
Run decision tree against sample data.
- Parameters
layers – tree output by
TreeTrainerdata – sample data (
Array)
- Returns
binary label
Compiler.circuit module¶
This module contains functionality using circuits in the so-called
Bristol Fashion format. You can download a few examples including
the ones used below into Programs/Circuits as follows:
make Programs/Circuits
- class Compiler.circuit.Circuit(name)[source]¶
Use a Bristol Fashion circuit in a high-level program. The following example adds signed 64-bit inputs from two different parties and prints the result:
from circuit import Circuit sb64 = sbits.get_type(64) adder = Circuit('adder64') a, b = [sbitvec(sb64.get_input_from(i)) for i in (0, 1)] print_ln('%s', adder(a, b).elements()[0].reveal())
Circuits can also be executed in parallel as the following example shows:
from circuit import Circuit sb128 = sbits.get_type(128) key = sb128(0x2b7e151628aed2a6abf7158809cf4f3c) plaintext = sb128(0x6bc1bee22e409f96e93d7e117393172a) n = 1000 aes128 = Circuit('aes_128') ciphertexts = aes128(sbitvec([key] * n), sbitvec([plaintext] * n)) ciphertexts.elements()[n - 1].reveal().print_reg()
This executes AES-128 1000 times in parallel and then outputs the last result, which should be
0x3ad77bb40d7a3660a89ecaf32466ef97, one of the test vectors for AES-128.
- class Compiler.circuit.ieee_float(value)[source]¶
This gives access IEEE754 floating-point operations using Bristol Fashion circuits. The following example computes the standard deviation of 10 integers input by each of party 0 and 1:
from circuit import ieee_float values = [] for i in range(2): for j in range(10): values.append(sbitint.get_type(64).get_input_from(i)) fvalues = [ieee_float(x) for x in values] avg = sum(fvalues) / ieee_float(len(fvalues)) var = sum(x * x for x in fvalues) / ieee_float(len(fvalues)) - avg * avg stddev = var.sqrt() print_ln('avg: %s', avg.reveal()) print_ln('var: %s', var.reveal()) print_ln('stddev: %s', stddev.reveal())
- Compiler.circuit.sha3_256(x)[source]¶
This function implements SHA3-256 for inputs of up to 1080 bits:
from circuit import sha3_256 a = sbitvec.from_vec([]) b = sbitvec.from_hex('cc') c = sbitvec.from_hex('41fb') d = sbitvec.from_hex('1f877c') e = sbitvec.from_vec([sbit(0)] * 8) f = sbitvec.from_hex('41fb6834928423874832892983984728289238949827929283743858382828372f17188141fb6834928423874832892983984728289238949827929283743858382828372f17188141fb6834928423874832892983984728289238949827') g = sbitvec.from_hex('41fb6834928423874832892983984728289238949827929283743858382828372f17188141fb6834928423874832892983984728289238949827929283743858382828372f17188141fb6834928423874832892983984728289238949827929283743858382828372f17188141fb6834928423874832892983984728289238949827929283743858382828372f171881') h = sbitvec.from_vec([sbit(0)] * 3000) for x in a, b, c, d, e, f, g, h: sha3_256(x).reveal_print_hex()
This should output the test vectors of SHA3-256 for 0, 8, 16, and 24 bits as well as the hash of the 0 byte:
Reg[0] = 0xa7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a # Reg[0] = 0x677035391cd3701293d385f037ba32796252bb7ce180b00b582dd9b20aaad7f0 # Reg[0] = 0x39f31b6e653dfcd9caed2602fd87f61b6254f581312fb6eeec4d7148fa2e72aa # Reg[0] = 0xbc22345e4bd3f792a341cf18ac0789f1c9c966712a501b19d1b6632ccd408ec5 # Reg[0] = 0x5d53469f20fef4f8eab52b88044ede69c77a6a68a60728609fc4a65ff531e7d0 # Reg[0] = 0xf5f673ec50d662039871fd53fae3ced069baf09030132d6d60d2ba7040b02b18 # Reg[0] = 0xa8a42e808f9dc0f43366d5de91511f42e9c3f8f37de0307f010bf629401edd2a # Reg[0] = 0xf722631013ecacd42b4c7259e9fe22b8c81a86e9fe0d4a626800e7f50c5a8978 #
Compiler.program module¶
This module contains the building blocks of the compiler such as code
blocks and registers. Most relevant is the central Program
object that holds various properties of the computation.
- class Compiler.program.Program(args, options=<class 'Compiler.program.defaults'>, name=None)[source]¶
A program consists of a list of tapes representing the whole computation.
When compiling an
.mpcfile, the single instance is available asprogram. When compiling directly from Python code, an instance has to be created before running any instructions.- property active¶
Whether to use actively secure protocols.
- join_tapes(thread_numbers)[source]¶
Wait for completion of tapes. See
new_tape()for an example.- Parameters
thread_numbers – list of thread numbers
- new_tape(function, args=[], name=None, single_thread=False)[source]¶
Create a new tape from a function. See
multithread()andfor_range_opt_multithread()for easier-to-use higher-level functionality. The following runs two threads defined by two different functions:def f(): ... def g(): ... tapes = [program.new_tape(x) for x in (f, g)] thread_numbers = program.run_tapes(tapes) program.join_tapes(threads_numbers)
- Parameters
function – Python function defining the thread
args – arguments to the function
name – name used for files
single_thread – Boolean indicating whether tape will never be run in parallel to itself
- Returns
tape handle
- run_tapes(args)[source]¶
Run tapes in parallel. See
new_tape()for an example.- Parameters
args – list of tape handles or tuples of tape handle and extra argument (for
get_arg())- Returns
list of thread numbers
- property security¶
The statistical security parameter for non-linear functions.
- use_dabit¶
Setting whether to use daBits for non-linear functionality.
- use_edabit(change=None)[source]¶
Setting whether to use edaBits for non-linear functionality (default: false).
- Parameters
change – change setting if not
None- Returns
setting if
changeisNone
- use_invperm(change=None)[source]¶
Set whether to use the low-level INVPERM instruction to inverse a permutation (see sint.inverse_permutation). The INVPERM instruction assumes a semi-honest two-party environment. If false, a general protocol implemented in the high-level language is used.
- Parameters
change – change setting if not
None- Returns
setting if
changeisNone
- use_split(change=None)[source]¶
Setting whether to use local arithmetic-binary share conversion for non-linear functionality (default: false).
- Parameters
change – change setting if not
None- Returns
setting if
changeisNone
- use_square(change=None)[source]¶
Setting whether to use preprocessed square tuples (default: false).
- Parameters
change – change setting if not
None- Returns
setting if
changeisNone
- property use_trunc_pr¶
Setting whether to use special probabilistic truncation.
Compiler.oram module¶
This module contains an implementation of the tree-based oblivious
RAM as proposed by Shi et al. as
well as the straight-forward construction using linear scanning.
Unlike Array, this allows access by a
secret index:
a = OptimalORAM(1000)
i = sint.get_input_from(0)
a[i] = sint.get_input_from(1)
- Compiler.oram.OptimalORAM(size, *args, **kwargs)[source]¶
Create an ORAM instance suitable for the size based on experiments. This uses the approach by Keller and Scholl.
- Parameters
size – number of elements
value_type –
sint(default) /sg2fn/sfix
Compiler.sqrt_oram module¶
- class Compiler.sqrt_oram.SqrtOram(data: Union[Compiler.sqrt_oram.T, Compiler.types.MultiArray], entry_length: int = 1, value_type: Type[Compiler.sqrt_oram.T] = <class 'Compiler.types.sint'>, k: int = 0, period: Optional[int] = None, initialize: bool = True, empty_data=False)[source]¶
Oblivious RAM using the “Square-Root” algorithm.
- Parameters
data (MultiArray) – The data with which to initialize the ORAM. One may provide a MultiArray such that every “block” can hold multiple elements (an Array).
value_type (sint) – The secret type to use, defaults to sint.
k (int) – Leave at 0, this parameter is used to recursively pass down the depth of this ORAM.
period (int) – Leave at None, this parameter is used to recursively pass down the top-level period.
Compiler.path_oblivious_heap module¶
This module contains an implementation of the “Path Oblivious Heap” oblivious priority queue as proposed by Shi.
Path Oblivious Heap comes in two variants that build on either Path ORAM
or Circuit ORAM. Both variants support inserting an element and extracting
the element with the highest priority in time \(O(\max(\log(n) + s, e))\) where \(n\)
is the queue capacity, \(s\) is the ORAM stash size, and \(e\) is the ORAM eviction
complexity. Assuming \(s = O(1)\) and \(e = O(\log(n))\), the operations are in \(O(\log n)\).
Currently, only the Path ORAM variant is implemented and tested (the PathObliviousHeap).
Furthermore, the UniquePathObliviousHeap class implements an update()
operation that is comparable to that of HeapQ from dijkstra, in that it ensures
that every value inserted in the queue is unique, and if update() is called
with a value that is already in the queue, the priority of that value is updated to be equal
to the new priority.
The following benchmark compares the online time of updating an element in HeapQ on top of Path
ORAM and updating an element in UniquePathObliviousHeap on top of Path ORAM. PathObliviousHeap
indeed seems to outperform HeapQ from around \(n = 2^4\).
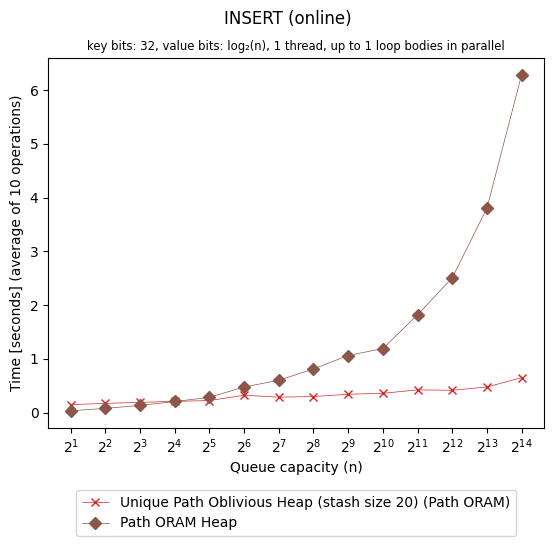
- class Compiler.path_oblivious_heap.POHToHeapQAdapter(max_size, *args, int_type=<class 'Compiler.types.sint'>, variant=POHVariant.PATH, bucket_size=None, stash_size=None, init_rounds=-1, entry_size=None, **kwargs)[source]¶
Adapts Path Oblivious Heap to the HeapQ interface, allowing plug-and-play replacement in the Dijkstra implementation.
- extract_min(fake: bool = False) Compiler.types._secret | None¶
Extract the element with the smallest (ie. highest) priority from the queue.
- find_min(fake: bool = False) Compiler.types._secret | None¶
Find the element with the smallest (ie. highest) priority in the queue and return its value and priority. Returns -1 if empty.
- insert(value, priority, fake: bool = False) None¶
Insert an element with a priority into the queue.
- pop(for_real=True)[source]¶
Renaming of pop to
extract_min().
- class Compiler.path_oblivious_heap.PathObliviousHeap(capacity: int, security: Optional[int] = None, type_hiding_security: bool = False, int_type: Type[Compiler.types._secret] = <class 'Compiler.types.sint'>, entry_size: Optional[Tuple[int]] = None, variant: Compiler.path_oblivious_heap.POHVariant = POHVariant.PATH, bucket_oram: Compiler.oram.AbstractORAM = <class 'Compiler.oram.TrivialORAM'>, bucket_size: Optional[int] = None, stash_size: Optional[int] = None, init_rounds: int = -1)[source]¶
A basic Path Oblivious Heap implementation supporting insert, extract_min, and find_min.
The queue is guaranteed to have at least the specified capacity with negligible error probability.
If inserting more entries than there is capacity for, the behavior depends on the value of the flag
oram.crash_on_overflow. If the flag is set, the program crashes. Otherwise, the entry is simply not inserted.- Variables
capacity – The capacity of the queue.
type_hiding_security – A boolean indicating whether type hiding security is enabled. Enabling this makes the cost of every operation equal to the sum of the costs of all operations. This is initially set by passing an argument to the class constructor.
int_type – The secret integer type of entry members.
entry_size – A tuple specifying the bit lengths of the entries in the order (priority, value).
- Iver tree
The MinTree data structure storing subtree-mins
- extract_min(fake: bool = False) Compiler.types._secret | None[source]¶
Extract the element with the smallest (ie. highest) priority from the queue.
- class Compiler.path_oblivious_heap.UniquePOHToHeapQAdapter(max_size, *args, int_type=<class 'Compiler.types.sint'>, variant=POHVariant.PATH, oram_type=<function OptimalORAM>, bucket_size=None, stash_size=None, init_rounds=-1, entry_size=None, **kwargs)[source]¶
Adapts Unique Path Oblivious Heap to the HeapQ interface, allowing plug-and-play replacement in the Dijkstra implementation.
- extract_min(fake: bool = False) Compiler.types._secret | None¶
Extract the element with the smallest (ie. highest) priority from the queue.
- find_min(fake: bool = False) Compiler.types._secret | None¶
Find the element with the smallest (ie. highest) priority in the queue and return its value and priority. Returns -1 if empty.
- insert(value, priority, for_real=True) None[source]¶
Insert an element with a priority into the queue.
- pop(for_real=True)[source]¶
Renaming of pop to
extract_min().
- class Compiler.path_oblivious_heap.UniquePathObliviousHeap(*args, oram_type=<function OptimalORAM>, init_rounds=-1, **kwargs)[source]¶
A Path Oblivious Heap that ensures that all values in the queue are unique and supports updating a value with a new priority by maintaining a value to leaf index map using ORAM.
- extract_min(fake: bool = False) Compiler.types._secret | None[source]¶
Extract the element with the smallest (ie. highest) priority from the queue.
- find_min(fake: bool = False) Compiler.types._secret | None¶
Find the element with the smallest (ie. highest) priority in the queue and return its value and priority. Returns -1 if empty.
- Compiler.path_oblivious_heap.path_oblivious_sort(keys: Compiler.types.Array, values: Compiler.types.Array, key_length: int, value_length: Optional[int] = None, **kwargs)[source]¶
Sort values in place according to keys using Path Oblivious Heap by calling insert followed by extract min.
Compiler.sorting module¶
- Compiler.sorting.radix_sort(k, D, n_bits=None, signed=True)[source]¶
Sort in place according to key.
- Parameters
k – keys (vector or Array of sint or sfix)
D – Array or MultiArray to sort
n_bits – number of bits in keys (int)
signed – whether keys are signed (bool)
- Compiler.sorting.reveal_sort(k, D, reverse=False)[source]¶
Sort in place according to “perfect” key. The name hints at the fact that a random order of the keys is revealed.
- Parameters
k – vector or Array of sint containing exactly \(0,\dots,n-1\) in any order
D – Array or MultiArray to sort
reverse – wether
keyis a permutation in forward or backward order